最优化技术——阅读报告

发表于 | 分类于 |

梯度下降——从批量下降到Nesterov加速法

如今，在神经网络魔性的训练过程中梯度下降被广泛的使用，它主要用于权重的更新，即对参数向某一方向进行更新和调整，来最小化损失函数。其主要原理是：

通过寻找最小值，控制方差，更新模型参数，最终使模型收敛。

什么是梯度？梯度是一个向量。函数在各个方向的斜率是方向导数，而斜率最大的方向是梯度，梯度的方向方向导数变化最快的方向。传统的梯度下降法对模型进行多次迭代，在迭代的过程中对模型参数进行更新，更新过程如下： \[ \theta=\theta−\alpha \frac{\partial J(\theta)}{\partial\theta} \tag{1} \] 其中，\(\alpha\)是学习率，\(J(θ)\)是损失函数，\(\frac{\partial J(\theta)}{\partial\theta}\)是梯度。学习率决定了权重更新的快慢，并且可以在凸面误差曲面中收敛到全局最优值，在非凸曲面中可能陷入局部最优值。

这篇文章会对梯度下降的发展进行简要概述，介绍该算法是如何从传统的梯度下降，逐步发展到Nesterov梯度下降加速法的。本文将以基本原理、代码实现、算法比较的流程进行展开。

小批量梯度下降

在文章最开始所说的梯度下降方法又被称为批量梯度下降算法将计算整个数据集梯度，但只会进行一次更新，因此在处理大数据集时迭代速度很慢且难以控制，甚至导致内存溢出。为解决这一问题，随机梯度下降方法诞生了。随机梯度下降（Stochastic Gradient Descent, SGD）每次从训练样本中随机抽取一个样本计算loss和梯度并对参数进行更新。

随机梯度下降算法解决了批量梯度下降算法中执行速度慢、内存消耗大的问题。但与此同时频繁的更新使得参数间具有高方差，损失函数会以不同的强度波动。与此同时，该方法受到异常数据影响较大。小批量梯度下降（Mini Batch Gradient Descent）可以避免SGD和标准梯度下降中存在的问题，因为对每个批次中的n个训练样本，这种方法只执行一次更新，它有如下优点：

  • 可以减少参数更新的波动
  • 可以通过矩阵优化来加速计算
  • 每次使用一个batch可以大大减小收敛所需要的迭代次数
  • 可以并行

动量（Momentum）

在前面的工作中，人们将关注点放在梯度下降的训练方式，即通过改变每次训练的数据的大小的方法，来均衡计算效率与计算的准确程度。但在迭代过程中，其更新方式都如1式所示。在这个方向上，小批量梯度下降已经非常优秀，想要继续对梯度下降法进行改进，就需要从别的方面进行考量。换句话说，就是如何利用现有的数据更好的更新参数？从公式上看，可以从梯度、学习率两个方面下手。

动量梯度下降法（Momentum）的基本的想法就是计算梯度的指数加权平均数，并利用该梯度更新你的权重。要想理解这一过程，我们需要从下面这张图来入手。

吴恩达
吴恩达

图中[1]的线条表示了梯度下降法在训练的过程中的路径，从初始点到终点的过程中，我们当然希望它能够直接向右进行平移，因为这样可以快速的到达目标点。但遗憾的是，由于梯度方向的影响，训练的过程如图所示，出现了非常严重的抖动现象。这种上下波动减慢了梯度下降法的速度，你就无法使用更大的学习率，如果你要用较大的学习率（紫色箭头），结果可能会偏离函数的范围，为了避免摆动过大，你要用一个较小的学习率。

从另外一个角度来看，你希望在纵轴方向上学习的慢一点，因为你不需要这些摆动；你还希望在横轴上学习的快一些，因为你希望快一点到达红点。想要做到这一点，我们需要做的事，对梯度进行修改，修改后的梯度如下： \[ v_d\theta=βv_d\theta+(1-β)d\theta \tag{2} \] 在更新时，使用\(v_dW\)进行更新，即： \[ \theta=\theta−\alpha v_d\theta \tag{3} \] 这样的方法能够将训练过程的中前面的训练信息与现在的训练信息进行综合，以提高训练速度。通常，其中的\(\beta\)常取0.9，使用动量法能够较快的到达终点，如下图[2]所示。

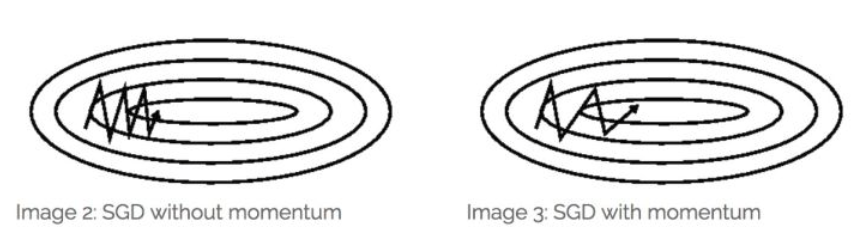
《An overview of gradient descent optimization algorithms》
《An overview of gradient descent optimization algorithms》

Nesterov梯度加速法

一位名叫Yurii Nesterov研究员，认为动量方法存在一个问题：

如果一个滚下山坡的球，盲目沿着斜坡下滑，这是非常不合适的。一个更聪明的球应该要注意到它将要去哪，因此在上坡再次向上倾斜时小球应该进行减速。实际上，当小球达到曲线上的最低点时，动量相当高。由于高动量可能会导致其完全地错过最小值，因此小球不知道何时进行减速，故继续向上移动。简单的说，就是由于物体存在惯性，所以物体的动量不会在到达最优点时直接消失，这就导致即使到了最优点还是会继续向错误的方向更新。

Nesterov梯度下降在动量法的基础上，又前进了一步，它的基本思想是：既然我都知道我这一次一定会走d_{i-1}的量，那么我何必还用现在这个位置的梯度呢？我直接先走到d_{i-1}之后的地方，然后再根据那里的梯度进行前进，于是就有了下面的公式： \[ d_i =\beta d_{i-1}+g(\theta_{i-1}-\alpha \beta d_{i-1}) \tag{4} \]

\[ \theta_i=\theta_{i-1}-\alpha d_{i} \tag{5} \]

算法代码

在这个分区中，我们以minist数据集为例，分别使用批量梯度下降、动量梯度下降、Nesterov梯度加速法进行训练，设置的模型较为简单，模型如下： \[ y = softmax(xW+b) \] 在模型的训练过程中，使用了批量一度下降的方法，将数据以100为单位进行分块，每次训练100条数据。以0.1的学习率训练150轮，通过观察下降的速度来评判算法。同时，为了避免随机数对算法的影响，我使用tf.set_random_seed(1)方法将训练过程中的随机种子固定。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import os
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "1"

import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
tf.set_random_seed(1)
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

sess = tf.InteractiveSession()
x = tf.placeholder(tf.float32,[None, 784])
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

y = tf.nn.softmax(tf.matmul(x,W)+b)

y_ = tf.placeholder(tf.float32,[None, 10])
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y),
                                              reduction_indices=[1]))
#train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cross_entropy)
#train_step = tf.train.MomentumOptimizer(0.1, momentum = 0.9, use_nesterov=True).minimize(cross_entropy)
#train_step = tf.train.MomentumOptimizer(0.1, momentum = 0.9).minimize(cross_entropy)
tf.global_variables_initializer().run()
acc = []
for i in range(150):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    train_step.run({x:batch_xs,y_:batch_ys})
    correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(y_,1))

    accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
    acc.append(accuracy.eval({x:mnist.test.images, y_:mnist.test.labels}))
print(accuracy.eval({x:mnist.test.images, y_:mnist.test.labels}))

import pylab as pl
pl.plot(acc)
pl.show()

对比

使用小批量梯度下降进行训练：

image-20200529155946624

使用动量梯度下降进行训练

image-20200529160041216

使用带有Nesterov梯度加速法的动量梯度下降进行训练

image-20200529160144255

可以看到，三种方法相比较下，小批量梯度下降的收敛速度明显低于另两种方法，这是由于其下降方向不准确，波动大而导致的。而使用简单的动量法时，在最优解附近发生了明显的正确率下降的情况，这是由于其惯性而导致的，通过对比，我们发现Nesterov梯度加速法的动量梯度下降进行训练的结果最优，其优秀主要体现在两个方面：

  • 收敛速度快
  • 在极值附近不会发生剧烈抖动

参考文献

[1] 吴恩达机器学习

[2] 《An overview of gradient descent optimization algorithms》