python图像处理笔记-十一-多视图重建与立体图像
多视图重建
由于照相机运动给我们提供了三维结构,所以这样计算三维重建的方法通常称作SFM (Structure from Motion,从运动中恢复结构)。我们假设摄像机已经标定,计算重建可以分为下面四个步骤:
检测特征点,在两幅图像中匹配
由匹配计算出基础矩阵
由基础矩阵计算照相机矩阵
三角形剖分这些三维点
我们前面已经把者四个东西都做过了,但是当图像间的点包含不正确的匹配关系时,需要一个文集爱你方法来估计矩阵。
稳健估计基础矩阵
类似于稳健计算单应性矩阵,存在噪声和不正确匹配的时候,我们需要估计基础矩阵,和前面的方法一样,使用RANSAC,不过这次结合了八点法。
我们写一段代码来实现它:
1 | # 归一化的八点法def compute_fundamental_normalized(x1,x2): """ 使用归一化的八点算法,由对应点(x1,x2 3×n 的数组)计算基础矩阵""" n = x1.shape[1] if x2.shape[1] != n: raise ValueError("Number of points don't match.") # 归一化图像坐标 x1 = x1 / x1[2] mean_1 = np.mean(x1[:2],axis=1) S1 = np.sqrt(2) / np.std(x1[:2]) T1 = np.array([[S1,0,-S1*mean_1[0]],[0,S1,-S1*mean_1[1]],[0,0,1]]) x1 = np.dot(T1,x1) x2 = x2 / x2[2] mean_2 = np.mean(x2[:2],axis=1) S2 = np.sqrt(2) / np.std(x2[:2]) T2 = np.array([[S2,0,-S2*mean_2[0]],[0,S2,-S2*mean_2[1]],[0,0,1]]) x2 = np.dot(T2,x2) # 使用归一化的坐标计算F F = np.compute_fundamental(x1,x2) # 反归一化 F = np.dot(T1.T,np.dot(F,T2)) return F/F[2,2]class RansacModel(object): def __init__(self, debug = False): self.debug = debug def fit(self, data): """ 使用选择的八个对应点计算基础矩阵 """ # 将数据分为两个点集 data = data.T x1 = data[:3, :8] x2 = data[3:, :8] # 估计基础矩阵并返回 F = compute_fundamental_normalized(x1,x2) return F def get_error(self, data, F): """ 计算所有对应的x^FFx,并返回误差 """ # 转置,将数据分为两个点集 data = data.T x1 = data[:3] x2 = data[3:] # 将Sampson距离用作误差度量 Fx1 = np.dot(F, x1) Fx2 = np.dot(F, x2) denom = Fx1[0] ** 2 + Fx1[1] ** 2 + Fx2[1] ** 2 + Fx2[0] ** 2 err = (np.diag(np.dot(F,x2))) ** 2 /denom return errdef F_from_ransac(x1, x2, model, maxiter = 5000, match_theshold = 1e-6): import ransac data = np.vstack((x1,x2)) # 计算F 返回正确点的索引 F, ransac_data = ransac.ransac(data.T, model, 8, maxiter, match_theshold, 20, return_all = True) return F, ransac_data['inliers'] |
三维重建实例:
老规矩,我们在来写个demo跑一下数据:
1 | from PCV.geometry import homographyfrom PCV.geometry import sfmfrom PCV.localdescriptors import siftfrom numpy import *from pylab import *from scipy import linalgfrom pylab import *from PIL import Image# 标定矩阵K = array([[2394,0,932],[0,2398,628],[0,0,1]])# 载入图像,并计算特征im1 = array(Image.open('alcatraz1.jpg'))sift.process_image('alcatraz1.jpg','im1.sift')l1,d1 = sift.read_features_from_file('im1.sift')im2 = array(Image.open('alcatraz2.jpg'))sift.process_image('alcatraz2.jpg','im2.sift')l2,d2 = sift.read_features_from_file('im2.sift')# 匹配特征matches = sift.match_twosided(d1,d2)ndx = matches.nonzero()[0]# 使用齐次坐标表示,并使用inv(K) 归一化x1 = homography.make_homog(l1[ndx,:2].T)ndx2 = [int(matches[i]) for i in ndx]x2 = homography.make_homog(l2[ndx2,:2].T)x1n = dot(inv(K),x1)x2n = dot(inv(K),x2)# 使用RANSAC 方法估计Emodel = sfm.RansacModel()E,inliers = sfm.F_from_ransac(x1n,x2n,model)# 计算照相机矩阵(P2 是4 个解的列表)P1 = array([[1,0,0,0],[0,1,0,0],[0,0,1,0]])P2 = sfm.compute_P_from_essential(E)# 选取点在照相机前的解ind = 0maxres = 0for i in range(4): # 三角剖分正确点,并计算每个照相机的深度 X = sfm.triangulate(x1n[:,inliers],x2n[:,inliers],P1,P2[i]) d1 = dot(P1,X)[2] d2 = dot(P2[i],X)[2] if sum(d1>0)+sum(d2>0) > maxres: maxres = sum(d1>0)+sum(d2>0) ind = i infront = (d1>0) & (d2>0) # 三角剖分正确点,并移除不在所有照相机前面的点 X = sfm.triangulate(x1n[:,inliers],x2n[:,inliers],P1,P2[ind]) X = X[:,infront]# 绘制三维图像from mpl_toolkits.mplot3d import axes3dfig = figure()ax = fig.gca(projection='3d')ax.plot(-X[0],X[1],X[2],'k.')axis('off')# 绘制X 的投影from PCV.geometry import camera# 绘制三维点cam1 = camera.Camera(P1)cam2 = camera.Camera(P2[ind])x1p = cam1.project(X)x2p = cam2.project(X)# 反K 归一化x1p = dot(K,x1p)x2p = dot(K,x2p)figure()imshow(im1)gray()plot(x1p[0],x1p[1],'o')plot(x1[0],x1[1],'r.')axis('off')figure()imshow(im2)gray()plot(x2p[0],x2p[1],'o')plot(x2[0],x2[1],'r.')axis('off')show() |
最后跑出来的结果如下:

立体图像
多视图成像的特殊例子是:立体视觉,它使用两台只有水平偏移的相机观测同一场景。
假设两张图片经过了矫正,那么对应点的寻找限制在图像的同一行上。一旦找到对应点,由于深度和偏移是成正比的,所以就可以通过水平偏移来计算深度:
\[ Z = \frac{fb}{x_l - x_r} \]
其中,f是矫正后图像的焦距,b是两个照相机中心之间的距离,\(x_l,x_r\)是左右两幅图像中,对应点的x坐标。分开摄相机中心的距离成基线,如下图所示:

立体重建是从两幅图像中恢复出深度图的work。
计算视差图
作者介绍了一种非常之暴力的方法,就是计算每一点取所有深度的代价,然后对于每个点取代价最小的选项,其中,度量在左图中取\(I_1\)点,右图中取\(I_2\)点的时候的代价的函数如下:
\[ ncc(I_1,I_2)=\frac{\Sigma_x((I_1(x)-\mu_1)(I_2(x)-\mu_2))}{\sqrt{\Sigma_x(I_1(x)-\mu_1)^2\Sigma_x(I_2(x)-\mu_2)^2}} \]
大家应该是学过概率论的,下面再普及几个概念(以听懂为目的,):
数学期望:
- \(EX = \Sigma P_ix_i\),相当于每件事发生的概率与发生时的值的乘积。
方差:
- \(DX = (EX^2)-E(X^2)\)
协方差:
\(Cov(X,Y) = E[(X-\mu_x)(Y-\mu_y)]\)
协方差越接近0,就说明两个量越相互独立
协方差是正数时,说明两个量正相关,反之则说明他们负相关
相关系数:
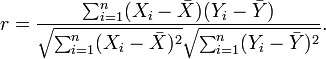
相关系数代表的是两个量之间的余弦值,这个值越接近0,就说明越不相关,反之则越相关。
所以上面的式子实际上在计算两个像素点附近的协方差,对图像周围的区域计算协方差能够计算出该点附近范围的相似性。
这个很简单,之前我做过类似的,所有就不在相同的事情上浪费时间了。