python图像处理笔记-七-图像扭曲与配准

对图像块使用仿射变换，我们将其称为图像扭曲。该操作不仅出现在计算机图形学中，还出现在计算机视觉算法中，扭曲可以用scipy的ndimage完成：

1	transformedIm = ndimage.affine_transform(im, A, b, size)

使用如上所示的线性变换A和一个平移向量B来对图像块进行仿射变换。选择参数size可以用来指定输出图像的大小。默认输出图像设置为和原始图像同样大小。为研究该函数是如何工作的，我们运行以下命令：

# -*- coding: utf-8 -*-
from PIL import Image
from numpy import *
from pylab import *
from scipy import ndimage

if __name__ == '__main__':
	im = array(Image.open('imgs/timg.jpg').convert('L'))
	H  = array([[1.4, 0.05, -100], [0.05, 1.5, -100], [0, 0, 1]])
	im2= ndimage.affine_transform(im, H[:2, :2],(H[0,2], H[1,2]))

	figure()
	gray()
	imshow(im2)
	show()

在这里，我们把之前那张铁塔的图做了一个扭曲，实质上我们用到的方法就是上一节讲到的仿射变换，其中，我们使用到的A、T矩阵是： \[ \left[ \begin{matrix} 1.4 &0.05 &-100\\ 0.05 &1.5 & -100\\ 0 & 0 & 1 \end{matrix} \right] \] 其中，旋转缩放矩阵与平移矩阵分别为： \[ A = \left[ \begin{matrix} 1.4 &0.05 \\ 0.05 &1.5 \end{matrix} \right] , T = \left[ \begin{matrix} -100 \\ -100 \end{matrix} \right] \] 图像经过扭曲后，输出如下，其中丢失的值使用零来填充：

接下来我们来简单地看一下这个ndimage.affine_transform(im, A, b, size)函数：

im ：需要进行变换的图像
A ：我们上面给出的A矩阵，主要负责图像的旋转、缩放等等
b ：我们上面给出的T，负责图像的平移
size ：目前还不知道

图像中的图像

放射扭曲的一个简单例子是：将图像或者图像的一部分放置在另一幅图像中，使他们能够和指定的区域或者标记物对齐。下面我们搞一个函数，它的输入参数是两幅图像和一个坐标，该坐标为第一幅图像放置第二幅图像中角点的坐标：

def imageInImage(im1, im2, tp):
	"""
	使用仿射变换将im1放置在im2上，使im1 图像的角点和tp尽可能靠近
	tp是齐次坐标，按照从左上角逆时针计算的
	"""
	# 扭曲的点
	m, n = im1.shape[:2]
	fp = array([[0, m, m, 0], [0, 0, n, n], [1, 1, 1, 1]])

	# 计算仿射变换,并将其用于图像im1
	# 这里掉了我们上个程序中写的包
	H = homoraphy.HaffineFromPoints(tp, fp)
	im1T = ndimage.affine_transform(im1, H[:2, :2], (H[0, 2], H[1, 2]),im2.shape[:2])

	alpha = (im1T > 0)

	return (1 - alpha) * im2 + alpha * im1T

现在我们的目标是这个样子的：

我们现在有两张图片：

第一张是我们的这个网页

第二张是我们从网上下载到的一个电脑的图片：

我们说，看这个星空多没意思，看我们博客的话，这个显示器的销量肯定能涨，那么接下来我们要把我们的博客加上去。首先，我们使用matplotlib.pyplot将这个电脑的图片打印出来，进行选点，当然了，如果我们每次都要重新手工取点，还要再更改程序的话，未免就有些太繁琐了，所以我们选用ginput()函数：

def getPoints(image, pointNum = 4, isChange = True):
	"""
	在image中取pointNum个点，如果ischange的话，那么就将点转换成齐次坐标
	最终返回获取到的点
	"""
	figure()
	gray()
	imshow(im)
	tempPoints = ginput(pointNum) # 取点
	x = []
	y = []
	for i in tempPoints:
		x.append(i[0])
		y.append(i[1])
	if(isChange == True):
		points = homoraphy.makeHomog(array([x,y])) # 将点转换成齐次坐标

	return points

运行该函数，我们可以在图像中选四个点：

选完四个点后，我们会将四个点的齐次坐标记录下来：

[[ 75.80458427 79.67916676 707.70405211 706.01624668] [151.9661478 518.80662682 526.25148681 107.01198678] [ 1. 1. 1. 1. ]]

最终我们将其次坐标导入我们的函数，即可完成我们想要的效果：

# -*- coding: utf-8 -*-
from PIL import Image
from numpy import *
from pylab import *
from scipy import ndimage
import homoraphy

def imageInImage(im1, im2, tp):
	"""
	使用仿射变换将im1放置在im2上，使im1 图像的角点和tp尽可能靠近
	tp是齐次坐标，按照从左上角逆时针计算的
	"""
	# 扭曲的点
	m, n = im1.shape[:2]
	fp = array([[0, m, m, 0], [0, 0, n, n], [1, 1, 1, 1]])

	# 计算仿射变换,并将其用于图像im1
	# 这里掉了我们上个程序中写的包
	H = homoraphy.HaffineFromPoints(tp, fp)
	im1T = ndimage.affine_transform(im1, H[:2, :2], (H[0, 2], H[1, 2]),im2.shape[:2])

	alpha = (im1T > 0)

	return (1 - alpha) * im2 + alpha * im1T


def getPoints(image, pointNum = 4, isChange = True):
	"""
	在image中取pointNum个点，如果ischange的话，那么就将点转换成齐次坐标
	最终返回获取到的点
	"""
	figure()
	gray()
	imshow(image)
	tempPoints = ginput(pointNum) # 取点
	x = []
	y = []
	for i in tempPoints:
		y.append(i[0])
		x.append(i[1])
	if(isChange == True):
		points = homoraphy.makeHomog(array([x,y])) # 将点转换成齐次坐标

	return points
if __name__ == '__main__':
	toImg = array(Image.open('imgs/Jindong.jpg').convert('L'))
	fromImg = array(Image.open('imgs/screen.png').convert('L'))
	points = getPoints(toImg)
	finalImg = imageInImage(fromImg, toImg, points)
	figure()
	gray()
	imshow(finalImg)
	show()

emm，还是有一些问题的，如果京东用了我们的照片的话，恐怕这款我最喜欢的显示器就要凉了，但是为了印证我们算法的准确性，我们还是需要找一张图片来找回点场子的：

我们按照刚才的方法，将我们博客的图片帖进去：

很好，这样的话，这款电脑的销量又被我们保住了，我们可真是“犹如天上降魔主,真是人间太岁神”这个算法，nb。但是又由此产生了一个疑问：为什么同一款显示器，对我的博客兼容性不一样呢？我们不难发现，这是由图像的透视效应决定的，很明显，正放的显示器透视效应不强，而刚才侧放的显示器透视效果就很强，那么我们再问自己，为什么会有透视效应？

很明显，所谓透视就是进大远小，而我们的博客，实际上是一个方方正正的矩形。而我们的仿射变换能够做到的只有：

平移、旋转、放缩、剪切、反射

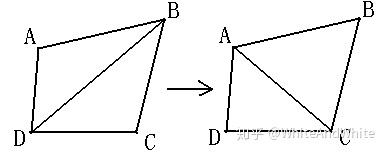
下面有一张图非常形象的告诉我们，仿射变换能够干什么：

很明显，这些性质都直接的无法与进大远小联系起来，所以我们说：

在具有很强透视效应的情况下，我们不可能使用同一个射影变换输出图像的情况。在这种情况下，我们不可能使用同一个仿射变换将全部四个角点变换到他们的目标位置。

对于这种情况，有一个很好的方法：

对于三个点，仿射变换可以将一幅图像进行扭曲，使这三对对应点可以玩美的匹配上，这是因为，仿射变换有6个自由度，三个对应点可以给出六个约束条件。所以如果在上述情况下，你可以将图像分解为两个三角形，然后分别对他们进行扭曲图像操作：

代码如下：

# -*- coding: utf-8 -*-
from PIL import Image
from numpy import *
from pylab import *
from scipy import ndimage
import homoraphy

def imageInImage(im1, im2, tp):
	"""
	使用仿射变换将im1放置在im2上，使im1 图像的角点和tp尽可能靠近
	tp是齐次坐标，按照从左上角逆时针计算的
	"""
	# 扭曲的点
	m, n = im1.shape[:2]
	fp = array([[0, m, m, 0], [0, 0, n, n], [1, 1, 1, 1]])

	# 计算仿射变换,并将其用于图像im1
	# 这里掉了我们上个程序中写的包
	H = homoraphy.HaffineFromPoints(tp, fp)
	im1T = ndimage.affine_transform(im1, H[:2, :2], (H[0, 2], H[1, 2]),im2.shape[:2])

	alpha = (im1T > 0)

	return (1 - alpha) * im2 + alpha * im1T


def getPoints(image, pointNum = 4, isChange = True):
	"""
	在image中取pointNum个点，如果ischange的话，那么就将点转换成齐次坐标
	最终返回获取到的点
	"""
	figure()
	gray()
	imshow(image)
	tempPoints = ginput(pointNum) # 取点
	x = []
	y = []
	for i in tempPoints:
		y.append(i[0]//1)
		x.append(i[1]//1)
	if(isChange == True):
		points = homoraphy.makeHomog(array([x,y])) # 将点转换成齐次坐标

	return points

def alphaForTriangle(points, m, n):
	"""
		对于带有points定义角点的三角形
		创建m，n的alpha
	"""
	alpha = zeros((m,n))
	for i in range(int(min(points[0])),int(max(points[0]))):
		for j in range(int(min(points[1])),int(max(points[1]))):
			x = linalg.solve(points, [i,j,1])
			if(min(x) > 0): # 所有系数都大于0
				alpha[i][j] = 1

	return alpha


def triangleImageInImage(im1, im2, tp):
	"""
	与上面不同的是：将im1分裂为了两个三角形进行变换
	"""
	# 扭曲的点
	m, n = im1.shape[:2]
	fp = array([[0, m, m, 0], [0, 0, n, n], [1, 1, 1, 1]])

	# 第一个三角形，前三个点：
	fp2 = fp[:,:3]
	tp2 = tp[:,:3]

	# 计算H
	# 这里掉了我们上个程序中写的包，将第一个三角形写入
	H = homoraphy.HaffineFromPoints(tp2, fp2)
	im1T = ndimage.affine_transform(im1, H[:2, :2], (H[0, 2], H[1, 2]),im2.shape[:2])

	# 三角形的alpha
	alpha = alphaForTriangle(tp2, im2.shape[0], im2.shape[1])

	im3 = (1 - alpha) * im2 + alpha * im1T

	# 第二个三角形
	fp2 = fp[:,[0,2,3]]
	tp2 = tp[:,[0,2,3]]

	# 计算H
	# 这里掉了我们上个程序中写的包，将第一个三角形写入
	H = homoraphy.HaffineFromPoints(tp2, fp2)
	im1T = ndimage.affine_transform(im1, H[:2, :2], (H[0, 2], H[1, 2]),im2.shape[:2])

	# 三角形的alpha
	alpha = alphaForTriangle(tp2, im2.shape[0], im2.shape[1])

	im4 = (1 - alpha) * im3 + alpha * im1T

	return im4

# 选定im1角上的一些点

if __name__ == '__main__':
	toImg = array(Image.open('imgs/Jindong.jpg').convert('L'))
	fromImg = array(Image.open('imgs/screen.png').convert('L'))
	points = getPoints(toImg)
	finalImg = triangleImageInImage(fromImg, toImg, points)
	figure()
	gray()
	imshow(finalImg)
	show()

结果如下：

对比刚才这个结果已经算得上是非常不错的了，但是我们发现，从三维空间考虑，我们对这个图片做的事情就是从中间对折了一下，这样就能与屏幕更适配了，但可惜的是，正是这种思想，导致两个三角形部分的缩放比不同，所以导致中间分隔线部分比较失真。但总体来说这个结果已经算得上是比较让人满意的了。

分段仿射扭曲

我们通过上面的例子发现，三角形图像块的仿射扭曲可以完成角点的精准匹配，然我们来看一下对应点对集合之间的最常用扭曲方式：分段放射扭曲。给定任意图像的标记点，通过将这些点进行三角形剖分，然后使用仿射扭曲来扭曲每一个三角形，我们可以将图像和另一幅图像的对应标记点扭曲对应。

为了三角化这些点，我们常用狄洛克三角剖分方法，下面我们简单的讲解下原理：

Delaunay三角剖分

参考

WhiteAndWhite 链接：https://zhuanlan.zhihu.com/p/42331420

三角形剖分定义

【定义】三角剖分：假设V是二维实数域上的有限点集，边e是由点集中的点作为端点构成的封闭线段, E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G，该平面图满足条件：

1.除了端点，平面图中的边不包含点集中的任何点。

2.没有相交边。

3.平面图中所有的面都是三角面，且所有三角面的合集是散点集V的凸包。

Delaunay三角剖分准则

空圆特性：Delaunay三角网是唯一的，任意四个点不能共圆。在Delaunay三角形网中任一三角形的外接圆范围内不会有其它点存在。
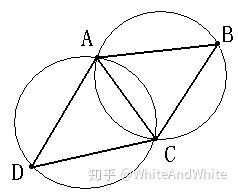
最大化最小角特性：在散点集可能形成的三角剖分中，Delaunay三角剖分所形成的三角形的最小角最大。从这个意义上讲，Delaunay三角网是“最接近于规则化的“的三角网。具体的说是指在两个相邻的三角形构成凸四边形的对角线，在相互交换后，六个内角的最小角不再增大。如下图所示：

下面我们来看最重要的部分

Bowyer-Watson算法

可以看这里：https://ui-mario.github.io/2019/11/29/Bowyer-Watson

为了效率和易用性，我们直接使用Scipy中的轮子就可以了（书中的matplotlib的我用不通不过问题不大）：

from scipy.spatial import Delaunay
from numpy import *
from pylab import *
points = array(standard_normal((100,2)))
tri = Delaunay(points)
triplot(points[:,0], points[:,1], tri.simplices.copy())
plot(points[:,0], points[:,1], 'o')
axis('off')
show()

结果如下：

我们看到这里根据点生成了很多的三角形，那么这如何与我们之前的东西结合起来呢？

我们知道三角形内的点能够完美的通过仿射变换被置换到其他图中
现在在原图中有很多点
原图中的点和新图中的很多点一一对应

有了上面这些东西我们的思路就非常的清晰了！我们希望能够将这些点整合成很多的三角形，这样就能更加精细的扭曲过去了，代码如下：

# -*- coding: utf-8 -*-
from PIL import Image
from numpy import *
from pylab import *
from scipy import ndimage
import homoraphy

def imageInImage(im1, im2, tp):
	"""
	使用仿射变换将im1放置在im2上，使im1 图像的角点和tp尽可能靠近
	tp是齐次坐标，按照从左上角逆时针计算的
	"""
	# 扭曲的点
	m, n = im1.shape[:2]
	fp = array([[0, m, m, 0], [0, 0, n, n], [1, 1, 1, 1]])

	# 计算仿射变换,并将其用于图像im1
	# 这里掉了我们上个程序中写的包
	H = homoraphy.HaffineFromPoints(tp, fp)
	im1T = ndimage.affine_transform(im1, H[:2, :2], (H[0, 2], H[1, 2]),im2.shape[:2])

	alpha = (im1T > 0)

	return (1 - alpha) * im2 + alpha * im1T


def getPoints(image, pointNum = 4, isChange = True):
	"""
	在image中取pointNum个点，如果ischange的话，那么就将点转换成齐次坐标
	最终返回获取到的点
	"""
	figure()
	gray()
	imshow(image)
	tempPoints = ginput(pointNum) # 取点
	x = []
	y = []
	for i in tempPoints:
		y.append(i[0]//1)
		x.append(i[1]//1)
	if(isChange == True):
		points = homoraphy.makeHomog(array([x,y])) # 将点转换成齐次坐标

	return points

def alphaForTriangle(points, m, n):
	"""
		对于带有points定义角点的三角形
		创建m，n的alpha
	"""
	alpha = zeros((m,n))
	for i in range(int(min(points[0])),int(max(points[0]))):
		for j in range(int(min(points[1])),int(max(points[1]))):
			x = linalg.solve(points, [i,j,1])
			if(min(x) > 0): # 所有系数都大于0
				alpha[i][j] = 1

	return alpha


def triangleImageInImage(im1, im2, tp):
	"""
	与上面不同的是：将im1分裂为了两个三角形进行变换
	"""
	# 扭曲的点
	m, n = im1.shape[:2]
	fp = array([[0, m, m, 0], [0, 0, n, n], [1, 1, 1, 1]])

	# 第一个三角形，前三个点：
	fp2 = fp[:,:3]
	tp2 = tp[:,:3]

	# 计算H
	# 这里掉了我们上个程序中写的包，将第一个三角形写入
	H = homoraphy.HaffineFromPoints(tp2, fp2)
	im1T = ndimage.affine_transform(im1, H[:2, :2], (H[0, 2], H[1, 2]),im2.shape[:2])

	# 三角形的alpha
	alpha = alphaForTriangle(tp2, im2.shape[0], im2.shape[1])

	im3 = (1 - alpha) * im2 + alpha * im1T

	# 第二个三角形
	fp2 = fp[:,[0,2,3]]
	tp2 = tp[:,[0,2,3]]

	# 计算H
	# 这里掉了我们上个程序中写的包，将第一个三角形写入
	H = homoraphy.HaffineFromPoints(tp2, fp2)
	im1T = ndimage.affine_transform(im1, H[:2, :2], (H[0, 2], H[1, 2]),im2.shape[:2])

	# 三角形的alpha
	alpha = alphaForTriangle(tp2, im2.shape[0], im2.shape[1])

	im4 = (1 - alpha) * im3 + alpha * im1T

	return im4


def pwAffine(fromim, toim, fp, tp, tri):
	"""
	从一幅图像中扭曲矩形图像块
	fromim  ：将要扭曲的图像
	toim    ：目标图像
	fp      ：齐次坐标表示下，扭曲前的点
	tp      ：齐次坐标表示下，扭曲后的点
	tri     ：三角形剖分
	:return im
	"""
	im = toim.copy()
	# 检查图像是否是彩色图，如果三通道，那么
	isColor = len(fromim.shape) == 3

	# 创建扭曲后的图像
	imT = zeros(im.shape, 'uint')
	for t in tri:
		# 计算仿射变换
		H = homoraphy.HaffineFromPoints(tp[:, t], fp[:, t])

		if isColor :
			for col in range(fromim.shape[2]-1):
				print(col)
				imT[:, :, col] = ndimage.affine_transform(
					fromim[:, :, col], H[:2, :2], (H[0,2], H[1,2]), im.shape[:2]
				)
		else :
			imT = ndimage.affine_transform(
				fromim, H[:2, :2], (H[0,2], H[1,2]), im.shape[:2]
			)

		# 三角形的alpha
		alpha = alphaForTriangle(tp[:, t], im.shape[0], im.shape[1])

		# 三角形加入到图像中
		im[alpha > 0] = imT[alpha > 0]

	return im


# 三角形剖分
def triangulatePoints(x,y):
	from scipy.spatial import Delaunay
	tri = Delaunay(c_[x,y]).simplices
	return tri


def plotMesh(x, y, tri):
	for t in tri:
		t_ext = [t[0], t[1], t[2], t[0]]
		plot(x[t_ext],y[t_ext], 'r')
if __name__ == '__main__':
	"""
	toImg = array(Image.open('imgs/Jindong.jpg').convert('L'))
	fromImg = array(Image.open('imgs/screen.png').convert('L'))
	points = getPoints(toImg)
	finalImg = triangleImageInImage(fromImg, toImg, points)
	figure()
	gray()
	imshow(finalImg)
	show()
	
	
	"""
	# 打开图像、扭曲
	fromim = array(Image.open('imgs/screen.png'))
	x, y = meshgrid(range(7), range(2))
	x = (fromim.shape[1] / 7) * x.flatten()
	y = (fromim.shape[0] / 2) * y.flatten()
	# 三角剖分
	tri = triangulatePoints(x, y)

	# 打开图像和目标点
	im = array(Image.open('imgs/Jindong.jpg'))
	imshow(im)
	tp =ginput(14)
	tp = array([[i[0],i[1]] for i in tp])

	# 将点转换成齐次坐标
	fp = vstack((y, x, ones((1,len(x)))))
	tp = vstack((tp[:, 1], tp[:, 0], ones((1,len(tp)))))
	# 扭曲三角形
	im = pwAffine(fromim, im, fp, tp, tri)
	figure()
	gray()
	imshow(im)
	plotMesh(tp[1], tp[0], tri)
	axis('off')
	show()

效果如下：

可以看到，结果依然很糟糕，但是之前的糟糕是因为技术原因而造成的，而这种糟糕是因为我手残而造成的，我们接下来多取一行点。

显然，效果更糟糕了，但显然，原因是我的手更残了。

图像的配准

图像配准是对图像进行变换，使变换后的图像能够在常见的坐标系中对齐。配准可以是严格配准，也可以是非严格配准。为了能够进行图像对比和更精细的图像分析，图像配准非常重要。

第一步：下载数据集

在之前的学习中，我一直用的自己的数据，这不是因为我特立独行，而是我实在不知道这玩意从哪里下。但是到了JKface这里，我就实在没办法了。在借着找不到数据集的原因滑了两天水之后，我竟然神奇的找到了整本书的数据集，下载方式如下，直接在shell里面：

1	wget http://programmingcomputervision.com/downloads/pcv_data.zip

在里面你就可以找到jkface.zip以及jkface.xml了。

第二步：xml数据读取

这个数据集是这个老哥每天给自己来一张自拍，在2008年拍了366天拍出来的，选一张效果如下

更厉害的是，不知道是谁，还对这366张照片的眼睛和嘴进行了标记，标记都保存在jkface.xml中/我们要做的事情就是：计算出一个相似变换，将可以使用该变换的这些图像扭曲到一个归一化的坐标系中。为了读取XML格式的文件，需要用到xml.dom模块中的minidom，下面我们来先看一下这个xml文件：

<?xml version="1.0" encoding="utf-8"?>
<faces>
	<face file="20080210.jpg" xf="127" xm="157" xs="189" yf="171" ym="247" ys="171"/>
	<face file="20080601.jpg" xf="132" xm="156" xs="186" yf="183" ym="238" ys="166"/>
	<face file="20080226.jpg" xf="137" xm="160" xs="183" yf="185" ym="238" ys="182"/>
.......

我们大概可以看出来：xml文件中记录了每个文件中左眼的坐标:\((xf,yf)\)，右眼的坐标\((xs,ys)\)，嘴的坐标\((xm,ym)\)，下面我们对它进行读入，由于上一小节的程序太长了，所以我们新开一个。

from xml.dom import minidom
from numpy import *
from PIL import Image
from pylab import *
from scipy import ndimage
import homoraphy

def readPointsFromXML(xmlFileName):
    """
    读取人脸的标记点
    """
    xmldoc = minidom.parse(xmlFileName)
    faceList = xmldoc.getElementsByTagName('face')
    faces = {}
    for xmlFace in faceList:
        fileName = xmlFace.attributes['file'].value
        xf = int(xmlFace.attributes['xf'].value)
        yf = int(xmlFace.attributes['yf'].value)
        xs = int(xmlFace.attributes['xs'].value)
        ys = int(xmlFace.attributes['ys'].value)
        xm = int(xmlFace.attributes['xm'].value)
        ym = int(xmlFace.attributes['ym'].value)
        faces[fileName] = array([xf, yf, xs, ys, xm, ym])
    return faces

temp = readPointsFromXML('C:\\Users\\wangsy\\Desktop\\opencvLearning\\jkDatas\\jkfaces.xml')
print(temp)

通过上面的函数，我们可以给出一个jkface.xml的路径，得到文件名与对应的坐标的字典。

扭曲

在这个数据集中，对于每个映射前的点\((x_i,y_i)\)与映射后的点\((\hat{x_i},\hat{y_i})\)，它们之间的关系可以表示为： \[ \left[ \begin{matrix} \hat{x_i}\\ \hat{y_i} \end{matrix} \right] = \left[ \begin{matrix} a & -b\\ b & a \end{matrix} \right] \left[ \begin{matrix} x_i\\ y_i \end{matrix} \right] + \left[ \begin{matrix} t_x\\ t_y \end{matrix} \right] \] 为什么这里的扭曲矩阵是这个样子的呢？，我们可以再来回顾一下这张图片：

我们这里对应着图片中第二行第一列的情况，但是在此基础上可能还会在cosθ和sinθ前面加上一个系数，这就说明我们在旋转的基础上还有可能做缩放，也就是说，上面的式子包含了：

旋转
缩放
平移

将三个点都写成上面的样子，在合到一起就是下面的样子了： \[ \left[ \begin{matrix} \hat{x_1}\\ \hat{y_1}\\ \hat{x_2}\\ \hat{y_2}\\ \hat{x_3}\\ \hat{y_3} \end{matrix} \right] = \left[ \begin{matrix} x_1 & -y_1 & 1 & 0\\ y_1 & x_1 & 0 & 1\\ x_2 & -y_2 & 1 & 0\\ y_2 & x_2 & 0 & 1\\ x_3 & -y_3 & 1 & 0\\ y_3 & x_3 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} a\\ b\\ t_x\\ t_y \end{matrix} \right] \] 上面我们也说了，可以使用相似矩阵的参数化表示方式： \[ \left[ \begin{matrix} a & -b\\ b & a \end{matrix} \right] = \left[ \begin{matrix} cos(\theta) & -sin(\theta)\\ sin(\theta) & cos(\theta) \end{matrix} \right] = s R \] 其中，尺度\(s = \sqrt{a^2+b^2}\)，旋转矩阵为\(R\)。

from xml.dom import minidom
from numpy import *
from PIL import Image
from pylab import *
from scipy import ndimage
import homoraphy
from scipy import linalg
import os
from imageio import imread, imsave

def readPointsFromXML(xmlFileName):
    """
    读取人脸的标记点
    """
    xmldoc = minidom.parse(xmlFileName)
    faceList = xmldoc.getElementsByTagName('face')
    faces = {}
    for xmlFace in faceList:
        fileName = xmlFace.attributes['file'].value
        xf = int(xmlFace.attributes['xf'].value)
        yf = int(xmlFace.attributes['yf'].value)
        xs = int(xmlFace.attributes['xs'].value)
        ys = int(xmlFace.attributes['ys'].value)
        xm = int(xmlFace.attributes['xm'].value)
        ym = int(xmlFace.attributes['ym'].value)
        faces[fileName] = array([xf, yf, xs, ys, xm, ym])
    return faces


def computeRigidTransform(refPoints, points):
    """
    计算用于将点对齐到参考点的RT矩阵
    """
    A = array([
        [points[0], -points[1], 1, 0],
        [points[1], points[0], 0, 1],
        [points[2], -points[3], 1, 0],
        [points[3], points[2], 0, 1],
        [points[4], -points[5], 1, 0],
        [points[5], points[4], 0, 1]
    ])
    y = array([
        refPoints[0],
        refPoints[1],
        refPoints[2],
        refPoints[3],
        refPoints[4],
        refPoints[5]
    ])
    a, b, tx, ty = linalg.lstsq(A,y)[0]
    R = array([[a, -b], [b, a]])
    return R, tx, ty


def rigidAlignment(faces, path, plotflag = False):
    """
    严格对齐图像，并将其保存为新的图像
    path : 决定对齐后图像的保存位置
    设置plotflag = True可以绘制图像
    """
    # 将第一幅图像中的点作为参考点
    refpoints = list(faces.values())[0]

    # 使用仿射变换扭曲每幅图像
    for face in faces :
        points = faces[face]
        R, tx, ty = computeRigidTransform(refpoints, points)
        T = array([[R[1][1], R[1][0]], [R[0][1], R[0][0]]])

        im = array(Image.open(os.path.join(path,face)))
        im2 = zeros(im.shape, 'uint8')

        # 对每个颜色通道进行扭曲
        for i in range(len(im.shape)):
            im2[:,:,i] = ndimage.affine_transform(im[:,:,i], linalg.inv(T), offset=[-ty, -tx])

        if(plotflag):
            imshow(im2)
            show()
        # 剪裁边界，进行保存
        h,w = im2.shape[:2]
        border = (w+h)//20

        # 保存
        imsave(os.path.join(path, 'aligned\\' + face), im2[border: h - border, border: w - border, :])

if __name__ == '__main__':
    xmlFileName = 'C:\\Users\\wangsy\\Desktop\\opencvLearning\\jkDatas\\jkfaces.xml'
    points = readPointsFromXML(xmlFileName)
    rigidAlignment(points, 'C:\\Users\\wangsy\\Desktop\\opencvLearning\\jkDatas\\jkfaces\\')

我们展示三组配准前后图像的区别：

配准前：

配准后：

可以看到图像中的人的眼睛、嘴巴是对齐了的，但是第三个图片我们感觉他的头是歪的，我个人认为造成这种现象的原因是：配准是根据人的眼睛、嘴巴来进行配准的，在这个过程可能出现以下误差：

手工标记时出现误差
眼、嘴对齐，但脸是歪的（局部最优）

为了避免该误差可以使用多个点来进行配准。