python图像处理笔记-六——单应性变换
齐次坐标
单应性变化是将一个平面内的店映射到另一个平面内的二维投影变换。本质上,单应性变换 H,按照下方的方程映射到二维的点:
\[ \left[\begin{matrix} x' \\ y' \\ w'\end{matrix}\right]=\left[\begin{matrix} h_1 & h_2 & h_3 \\ h_4 & h_5 & h_6 \\ h_7 & h_8 & h_9\end{matrix}\right]\left[\begin{matrix} x \\ y \\ w\end{matrix}\right] \] 我们也可以表示为: \[ x' = Hx \] 对于图像平面内的点,齐次坐标是一个非常有用的表示方式。点的齐次坐标是依赖于其尺度定义的,所以以下三种表述实质上都在表示同一个二维点。 \[ \begin{align} x &= [\begin{matrix} x & y& w\end{matrix}] \\ &= [\begin{matrix} \alpha x & \alpha y& \alpha w\end{matrix}] \\ &= [\begin{matrix} x/w & y/w& 1\end{matrix}] \end{align} \]
因此单应性矩阵H也仅依赖尺度定义,所以单应性矩阵具有八个独立的自由度。我们常用\(w = 1\)来归一化点,这样点就会拥有唯一的坐标:x和y。如果你看过我写的组成原理笔记的话,你会发现这里的目的和浮点数的左归、右归那里的目的非常相似。这个额外的坐标使得我们可以简单地使用一个矩阵来表示变换。
仿射变换
在投影变换中,有一些特别重要的变换,如:仿射变换: \[ \left[\begin{matrix} x' \\ y' \\ 1\end{matrix}\right]= \left[\begin{matrix} a_1 & a_2 & t_x \\ a_3 & a_4 & t_y \\ 0 & 0 & 1\end{matrix}\right] \left[\begin{matrix} x \\ y \\ z\end{matrix}\right] \] 或者我们也可以写作: \[ x' = \left[\begin{matrix}A & t \\ 0 & 1\end{matrix}\right] x \] 我们来实现一下这个仿射变换的代码:
1 | from PIL import Image |
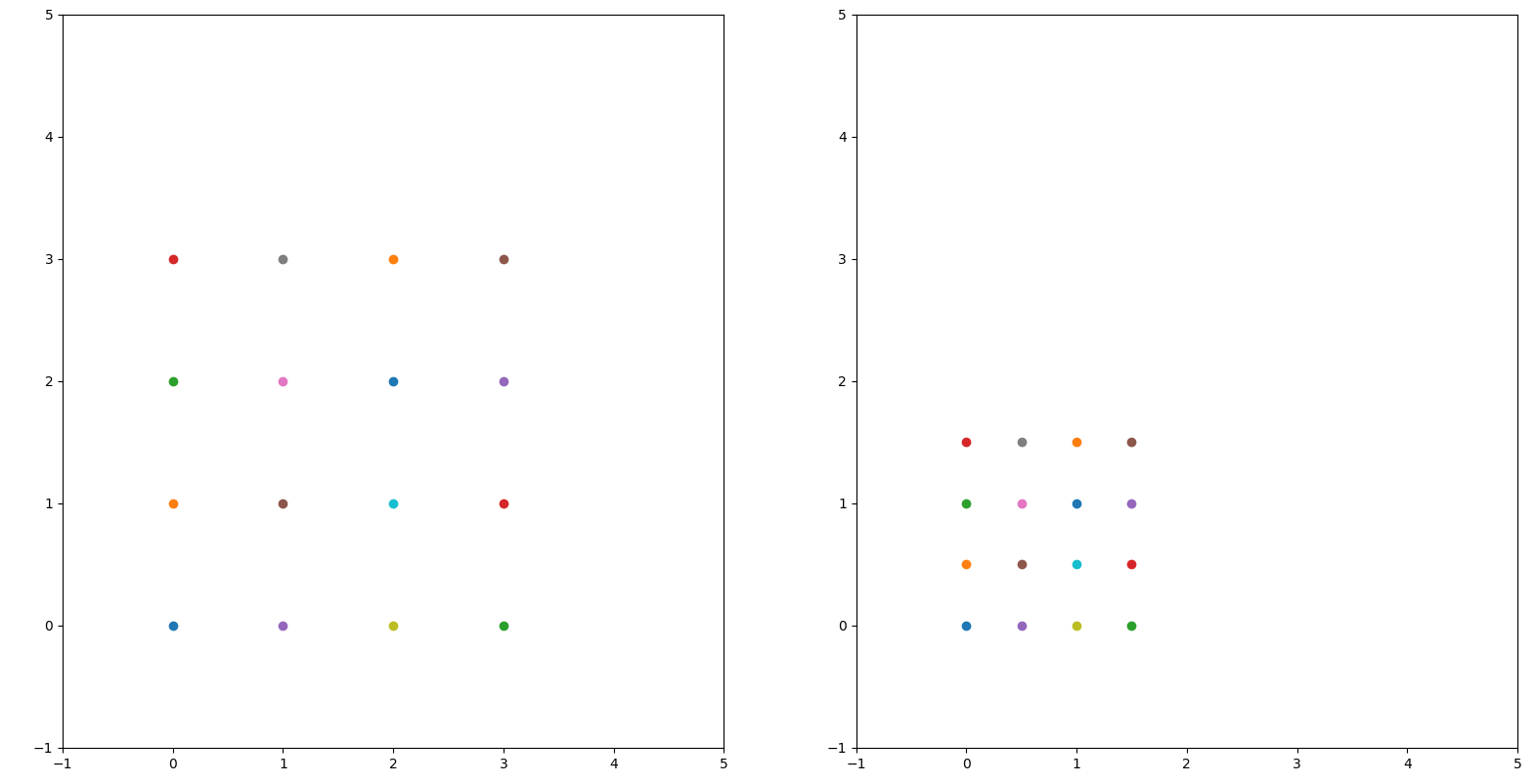 上面的图像中我们对左边的图像使用矩阵: \[
\left[
\begin{matrix}
0.5 &0 &0\\
0 &0.5 & 0\\
0 & 0 & 1
\end{matrix}
\right]
\] 进行仿射变换,我们发现图像变小了,于是我们知道左边的A可以控制图像的大小。随后,我们将矩阵修改为: \[
\left[\begin{matrix}0.5 &0 &1\\0 &0.5 & 1\\0 & 0 & 1\end{matrix}\right]
\]
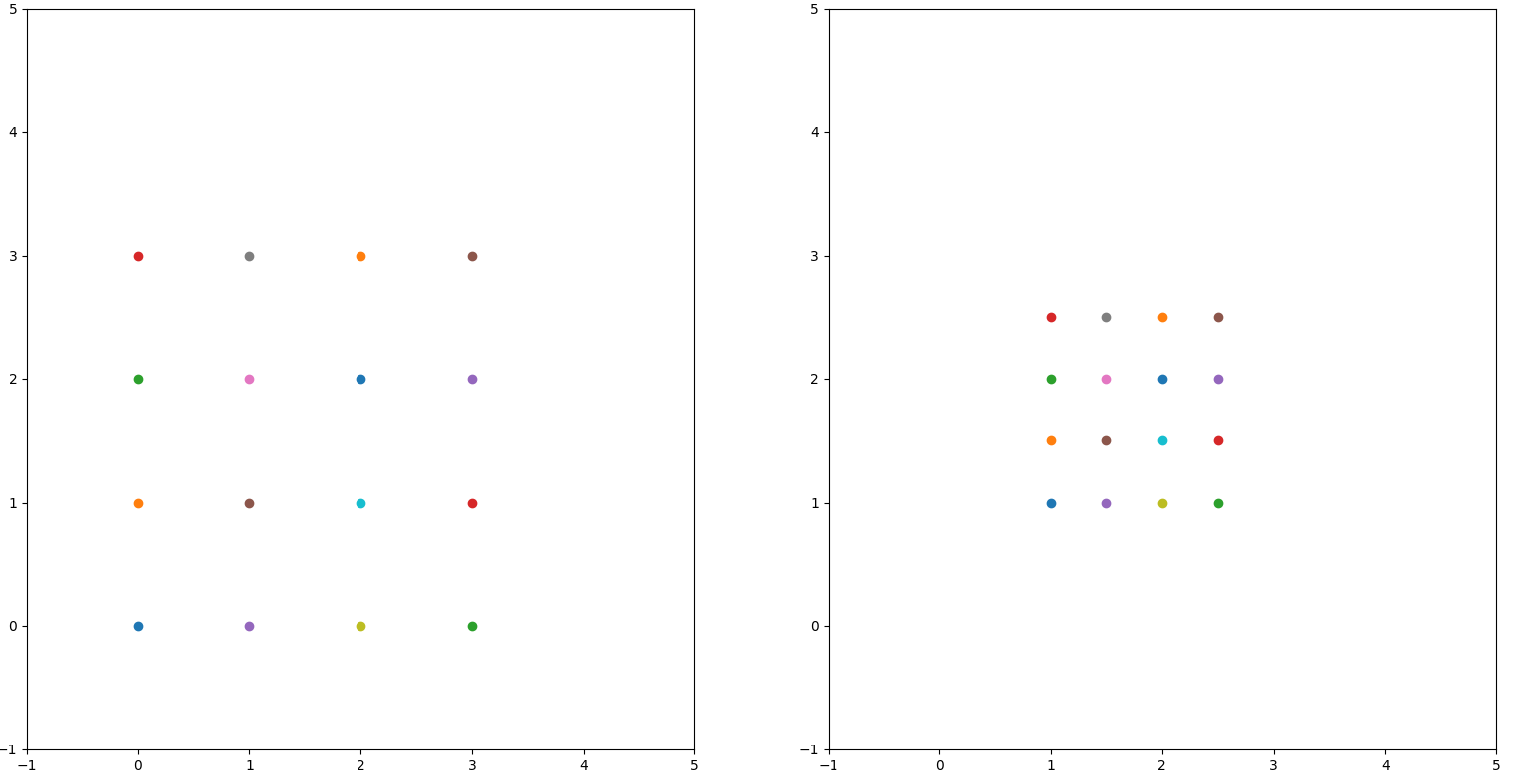
上面的图像中我们对左边的图像使用矩阵: \[
\left[
\begin{matrix}
0.5 &0 &0\\
0 &0.5 & 0\\
0 & 0 & 1
\end{matrix}
\right]
\] 进行仿射变换,我们发现图像变小了,于是我们知道左边的A可以控制图像的大小。随后,我们将矩阵修改为: \[
\left[\begin{matrix}0.5 &0 &1\\0 &0.5 & 1\\0 & 0 & 1\end{matrix}\right]
\]
 我们发现之前说的T能够控制图像的平移,实际上它还可以控制图像的旋转等,我在网上看到一张图,和大家分享一下:
我们发现之前说的T能够控制图像的平移,实际上它还可以控制图像的旋转等,我在网上看到一张图,和大家分享一下:
除此之外还有相似变换,相似变换是一种特殊的仿射变换,他描述了图像的旋转、平移、缩放,可以表示为:
\[ \left[ \begin{matrix} x'\\ y'\\ 1 \end{matrix} \right] = \left[ \begin{matrix} s *cos(\theta) & -s *sin(\theta) & t_x\\ s *sin(\theta) & -s *cos(\theta) & t_x\\ 0&0 & 1 \end{matrix} \right] \left[ \begin{matrix} x\\ y\\ 1 \end{matrix} \right] \]
直接线性变换算法
单应性矩阵可以由两幅图像中对应点计算出来。一个完全摄影变换有8个自由度。根据对应点约束,每个对应点可以写出两个方程,分别对应于\(x,y\)坐标。因此计算单应性矩阵H需要四个对应点对。
DLT(Diret Linear Transformation, 直接线性相似变化)是给定4个或者更多对应点对矩阵,来计算单应性矩阵H的方法。将单应性矩阵H作用在对应点上,重新写出该方程,我们可以得到下方方程:

我们可以看到,实际上用一组也可以解出结果,但是为了解的稳定,我们最好使用四组以上的特征匹配。方程的最小二乘解有一个既定的结论,即对A进行SVD分解,A的最小的奇异值对应的右奇异向量即是h的解。对h做reshape得到H。
直接线性变换算法在普通情况下,有八个自由度,而在解决仿射变换时,只有六个自由度,我们分别对两种情况写了代码:
1 | from PIL import Image |
结果
在刚才的代码中,我们使用仿射变换矩阵: \[ \left[\begin{matrix}0.5 &0 &1\\0 &0.5 & 1\\0 & 0 & 1\end{matrix}\right] \] 进行变化,我们利用一组点变换前后的状态,求仿射变换矩阵。得到的结果如下:
[[ 5.00000000e-01 1.20777603e-16 1.00000000e+00] [-1.13154271e-16 5.00000000e-01 1.00000000e+00] [ 2.45515188e-17 1.40739819e-17 1.00000000e+00]]
[[ 5.00000000e-01 6.07529133e-16 1.00000000e+00] [-1.11022302e-16 5.00000000e-01 1.00000000e+00] [ 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
其中,上面的结果是8自由度下的解,而下面的结果是6自由度下的解。我们可以发现结果非常完美。但是这是否是由于我门取了4*4=16个点的原因呢?于是我降低了采样数量,从原来的采样间隔为1降低到采样间隔为2,并进行观察。在此情况下,我们只取4个点,结果如下:
[[ 5.00000000e-01 -3.12481436e-16 1.00000000e+00] [-5.50986389e-16 5.00000000e-01 1.00000000e+00] [-3.84592537e-16 -9.61481342e-17 1.00000000e+00]]
[[ 5.00000000e-01 -1.79637859e-16 1.00000000e+00] [ 1.11022302e-16 5.00000000e-01 1.00000000e+00] [ 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
我们发现,虽然结果与上一组相比较下,偏差相对较大,但是误差仍然在可以忽略的范围内,总体来说结果非常理想。