计算机组成原理—第三章
参考资料
《计算机组成与设计:硬件/软件接口》——机械工业出版社
《Arithmetic for Computers》——Jiang Zhong
授课内容 —— 吴长泽老师
ALU的构建
ALU就是运算器,这些内容都可以在书中的附录中找到,我们接下来看一个简单的例子
逻辑的与、或
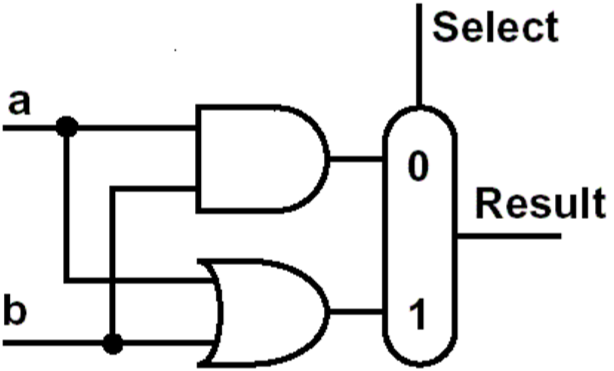
可以看到,这里有两个输入,a、b,他们分别连接到了一个与门和一个或门,他们分别与和或的结果又连接到了一个多路选择器上,Select用于控制到底是做与运算还是做或运算,Select = 0时,做与,Select = 1的时候我们就做或运算。
回归正题,加法——半加器
为了达到计算的目的,我们需要构建最基础的运算单元,那就是半加器。半加器是什么?半加器可以接收两个相加的数,然后给出他们相加的和以及他们的进位,但是他没有接受低位的进位,所以它叫半加器。
graph LR a --> halfAdder b --> halfAdder halfAdder --> sum halfAdder --> carry
我们先来构建一个真值表:
根据真值表可以构建出表达式:
$$
Sum = b +a\
Carry = ab
$$
根据表达式可以构建出电路:
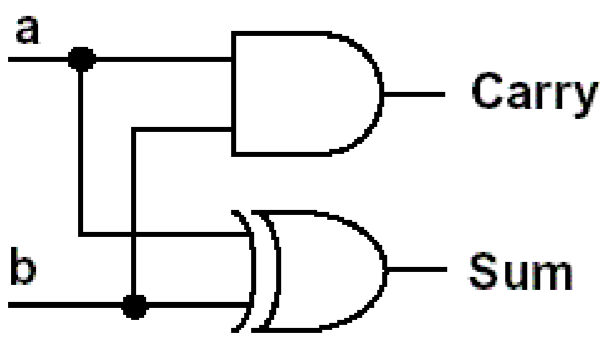
全加器
真值表
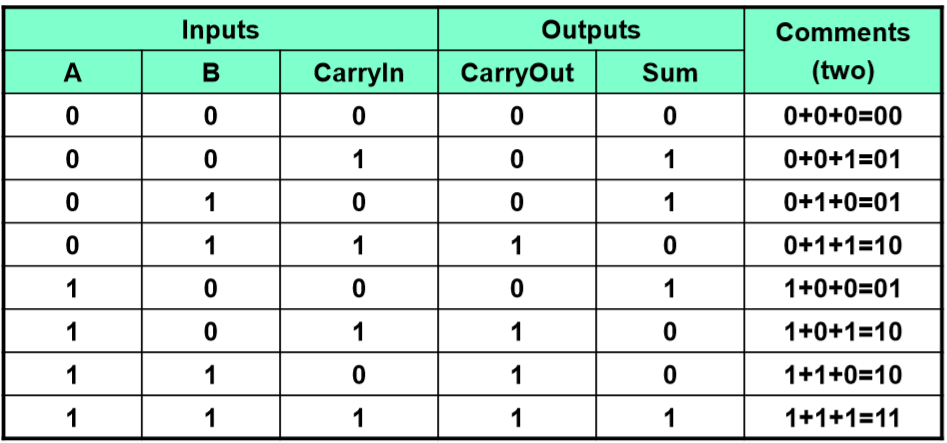
表达式
$$
Sum = A xor B xor CarryIn \
CarryOut = B CarryIn + A CarryIn + A B
$$
电路
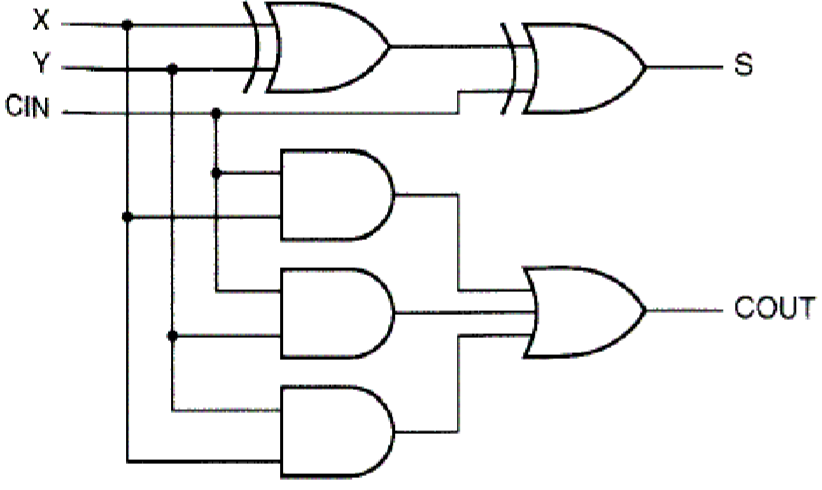
有了加法器之后,我们就可以做很多的运算了,以加法为例,只需要将很多全加器串在一起就可以构成一个多位整数的加法器。
1 bit ALU
有了上面的这些积累之后,我们就可以实现一个有以下功能的ALU:
AND
OR
ADD
其实实现的方法也非常简单,就是对刚才的多路选择器做一个拓展,把全加器加进来就可以了。
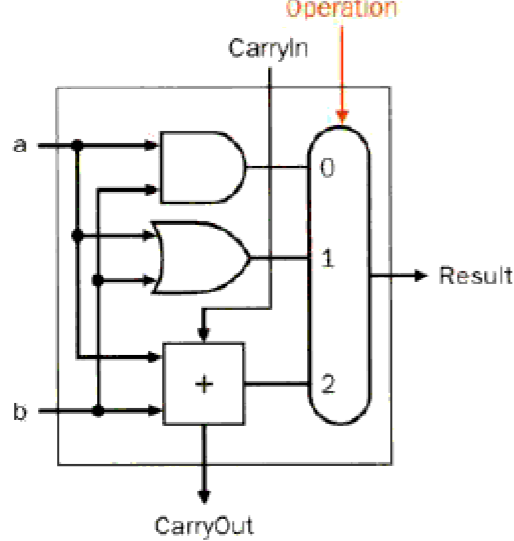
Basic 32 bit ALU
那么有了一个1 bit ALU之后,就可以把32个1 bit ALU级联在一起,就可以形成一个32位的ALU
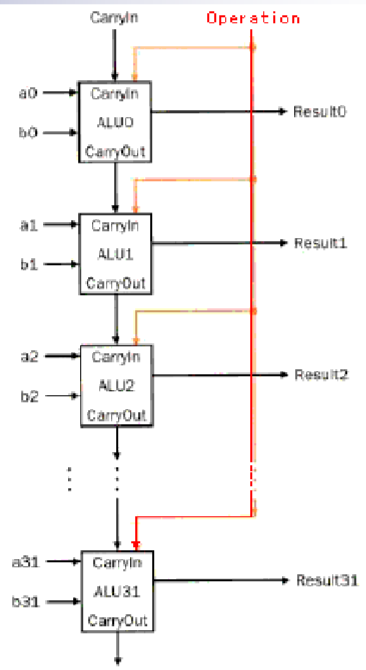
但是值得注意的是,级联的运算器的数目越多,它的体积、成本以及出错概率都会相应的上升,他的可靠性、成本都会有所下降,所以往往不会以1bitALU为基础进行级联,而是会以多位的ALU为基础在进行级联,这样能够降低成本、增加准确率。
扩展1 bit ALU
我们还希望我们的这个ALU可以完成减法操作,那么应该怎么做呢?我们都知道,假如说要完成\(a-b\)的操作,那么实际上完成的是\(a\)加上\(b\)的补码。\(b\)的补码就是对\(b\)进行取反,然后加一。那么这一系列的操作反应在电路中实际上就是:
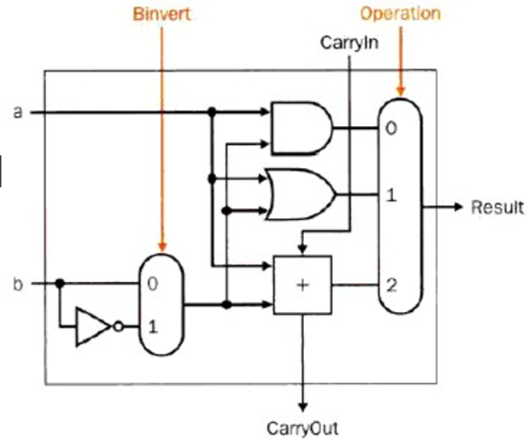
如果我们要进行减法运算,那么我们就需要将\(Binvert\)设置为1这样就完成了对b的取反操作,同时,我们需要将最低位的\(Carryin\)的值改为1,就可以完成上面说的加一的操作。这样我们在没有添加过多的逻辑单元的情况下就完成了从加法器到加法、减法器的扩展。
那么经过扩展后,我们的功能有:
AND
OR
ADD
Subtract
我们发现缺少了比较操作:
Slt rd, rs, rt; 也就是比较功能
如果rs < rt, rd = 1 否则 为0
那么怎么去做呢?我们可以是用减法来完成这一功能,我们可以做\(rs - rt\)的操作,如果结果是负数,那么就表示\(rs<rt\)。接下来看电路:
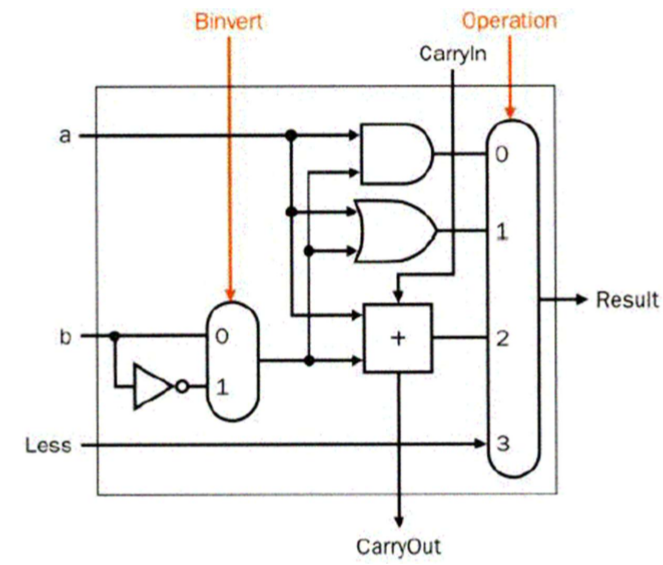
这里的less是负责接收高位信息的,因为我们在判断两个多位整数的大小的时候,是不能通过低位去判断的,所以我们需要这种机制来进行。大家觉得没讲透的话可以继续往下看,一会会讲到级联后的这个,到时候会好理解一些。
那么除了设置比较之外,我们还需要去做一个溢出探测。溢出是指有限的符号位无法表示我们的结果了。溢出是通过最高位和符号位进行判断。
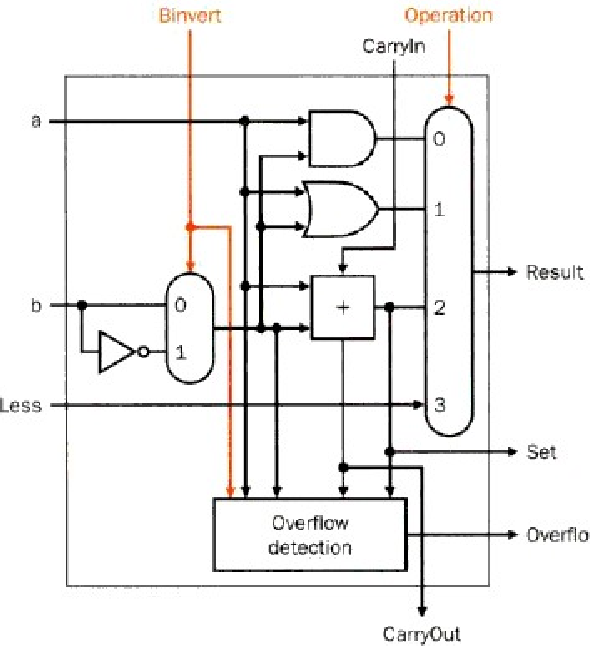
这里也是先挖个坑,等下再来填。
Compute ALU
输入:
A
B
控制量:
Binvert:是否反转
Operation:选择做什么运算的,其实就是那个选择器
Carryin:上一个数的进位
输出:
Result
Overflow
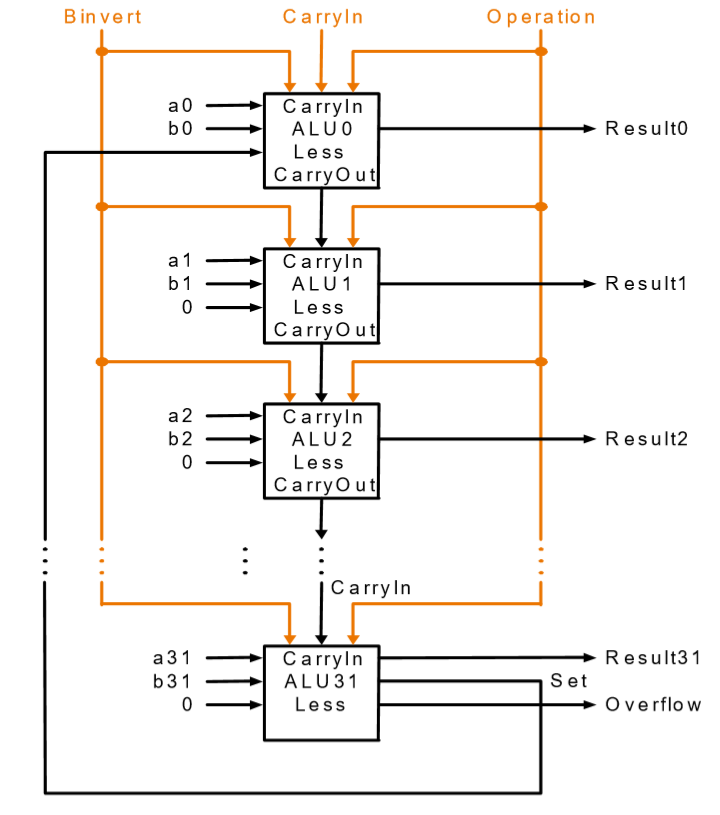
哒哒哒敲黑板开始填坑了:观察这个电路我们可以发现,高位的结果连接到了最低位的Less上,如果\(Operation\)是加法而且\(Binvert\)是1也就是进行反转,而且\(Carryin\)是1的话,就代表着我们在做A-B的操作。A-B后,如果高位是1的话,那么就说明A>B,否则就说明\(A \leq B\),这样就完成了简单的判断大小的操作。
如果到这里你还是看不懂,那么不慌,我们详细的讲一下,假如说我们现在有两个4位有符号数A = 3,B=4
我们要对比它们的大小,那么就需要先进行A-B的操作,为执行该操作,我们先对B进行取补码的操作:
B = \(0100_2\)
\(B_补=not(0100) + 0001 = 1011+0001=1100\)
\(A-B = A+B_补 = 0011+1100 = 1111\)最高位为1,说明A<B
接下来看第二种情况,\(A=4,B=3\),判断A、B大小
B = \(0011_2\)
\(B_补=not(0011_2) + 0001_2 = 1100_2+0001_2=1101_2\)
\(A-B = A+B_补 = 1101_2 + 0100_2 = 0001_2\),最高位为0,说明\(A \not < B\)
相信大家一定看懂了,如果看不懂,那就把上面的部分再看一遍,还是看不懂建议再去复习一下二进制表示部分的内容。接下来还需要增加一个功能,因为我们时常需要判断相加的结果是否为0,所以我们想要添加一个判断是否为0的门,原理也很简单,如果每一位都是0的话,那么结果也一定为0,把人话翻译成机器语言就是所有Result进行或运算,如果是0的话那么就说明都是0,反之就说明不是0,那么对结果取反后,如果不是0那么就输出1,反之就是0,电路如下。

ALU symbol & control
我们将上面的级联电路进行封装,就得到了一个ALU,示意图如下:
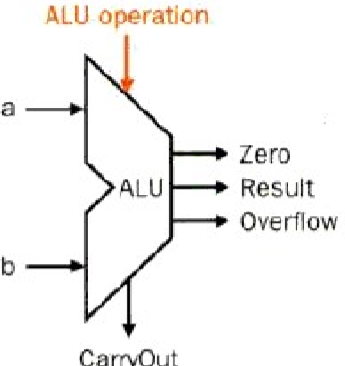
ALU operation的值与其对应的操作如下:
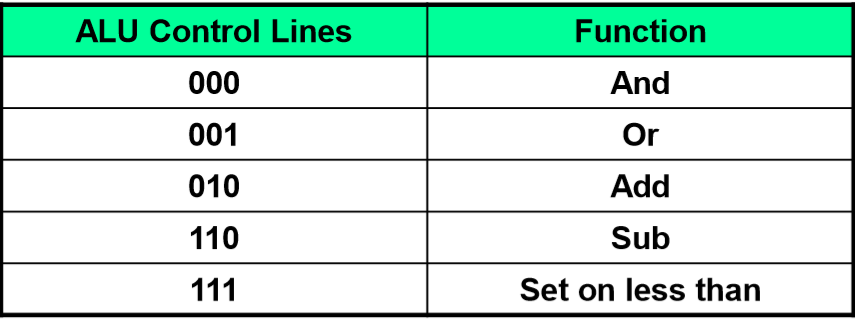
ALU的构建部分到此结束了。
整数加减法
数的表示范围:
有一个n位的二进制整数
有符号:
正数:\(2^{n-1}-1\)
负数:\(2^{n-1}\)
无符号:\(2^n-1\)
什么样子的数进行运算会溢出呢?
正数负数相加:不会发生溢出
两个正数相加:可能溢出
两个负数相加:可能溢出
整数的减法
很简单,我们上面也有所提及,\(A-B=A+B_补\),在这里我们主要讨论在什么情况下会发生溢出。
什么时候溢出?
两个正数相减或两个负数相减:不会溢出,因为结果的绝对值一定比两者绝对值一定比两者绝对值的最大值小,人话听不懂,但是用数学语言描述就看得懂了:
$$
if (A0 B0)(A0 B0):\
|A-B|max(|A|,|B|)
$$
正数减负数:可能发生溢出
负数减正数:可能发生溢出
溢出处理
发生溢出的时候,通常的做法是:将PC的值存到EPC中,其中PC的值代表当前指令,EPC代表发生错误的指令,执行这步操作,实际上在干的事情就是:记录下来,这个语句出错了。
\(mfc0\)指令可以进行异常处理并且返回到当前指令继续执行。
加法器的速度问题
问题
常用的方法是使用串行的处理方式,也就是先计算低位,然后从低位到高位依次计算,如下图所示:
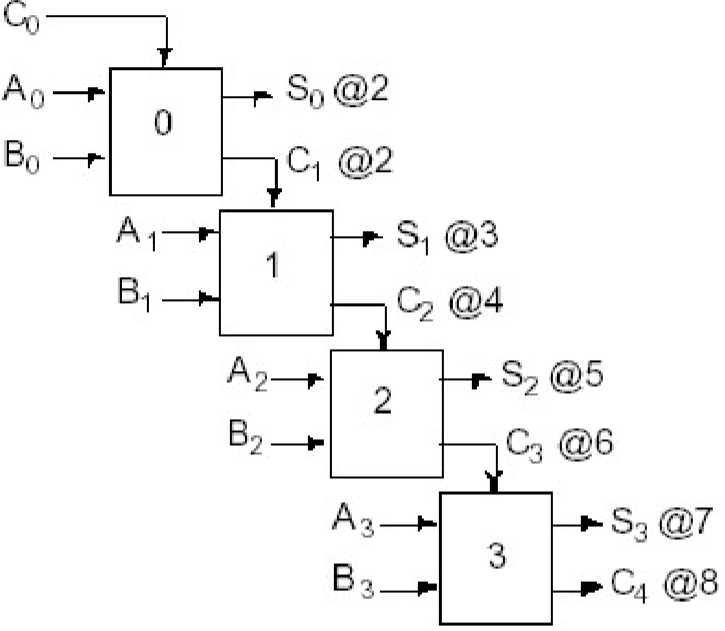
这样计算的效率很低,这是由于后方的运算需要等待前方的进位完成才能够进行计算。如果我们能够预先知道上一位的进位的话,就可以极大地加快效率。
解决
我们可以将这个串行的电路改成一个两层的逻辑,这样可以极大的提升他的计算速度,但是这样的改动是有巨大的代价的,代价就是:需要很多的输入门,导致电路的体量很大。下面有一些解决方案:
超前进位加法器
核心思路:将需要进位的值和计算的值进行分离。
$$
Generate : g_i = a_i*b_i
$$
$$
Propagate : p_i = a_i xor b_i
$$
我们先来看上面的两个符号,\(Generate\)代表当前位的结果,\(Propagate\)代表当前位的进位。我们很容易得到当前位的结果为\(a_i\ xor\ b_i\),进位的结果是\(a_i \and b_i\)。
接下来我们再来关注一下上一位的进位和最终结果之间的关系,我们定义符号\(C_i\)表示来自上一位的进位
接下来我们来写一下这个表达式:
$$
\[\begin{align} \begin{array} CC &= (c_i\and b_i\and not(a_i)) \or (a_i\and not(b_i)\and c_i)\or(a_i\and b_i\and not(c_i))\or (a_i\and b_i\and c_i) \end{array} \end{align}\]
$$
我们将这个表达式进行化简,就可以得到最终的结果:
$$
C_0 = (a xor b )c + ab
$$
计算过程如下( 写字烂,勿喷),由于篇幅原因这里省略了很多中间步骤:

根据这个过程我们可以构造出相应的全加器电路:
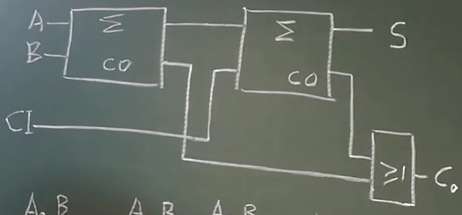
下面的图中给出了超前进位加法,在多位运算中的式子:
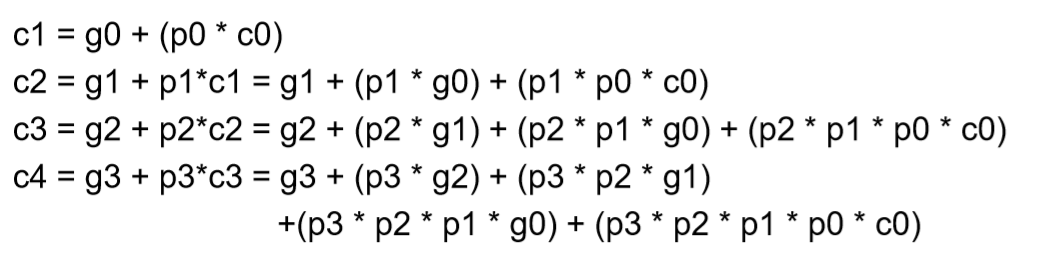
我们可以把原来串行的加法器拆分成四个一组,在每一组中进行超前进位加法,然后再将多个四位的超前进位加法器级联在一起,就可以达到使计算速度增加,但又不过度使用计算资源的效果。

下图所示的是一个四位的超前进位加法器:
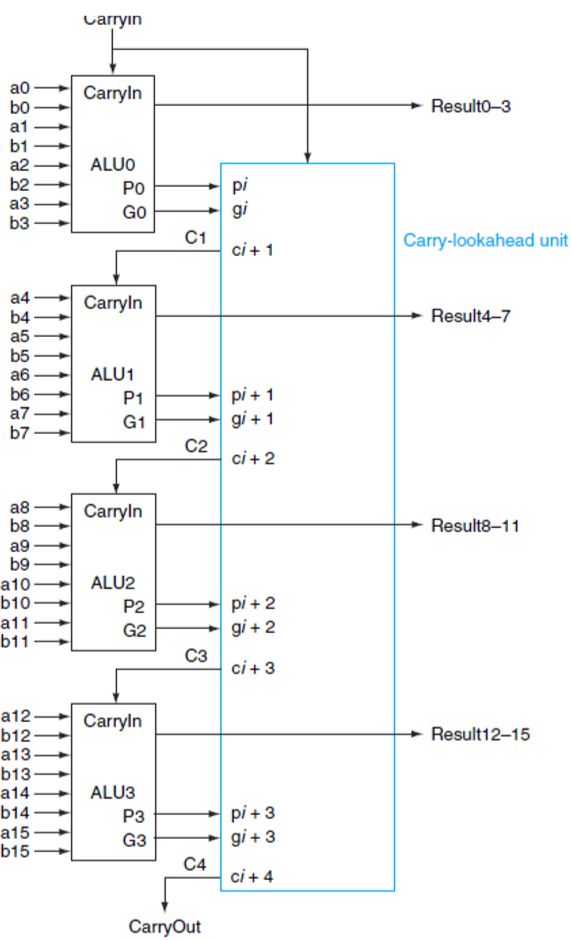
我们可以对他进行封装,并且进行级联即可获得更高位的快速加法器:
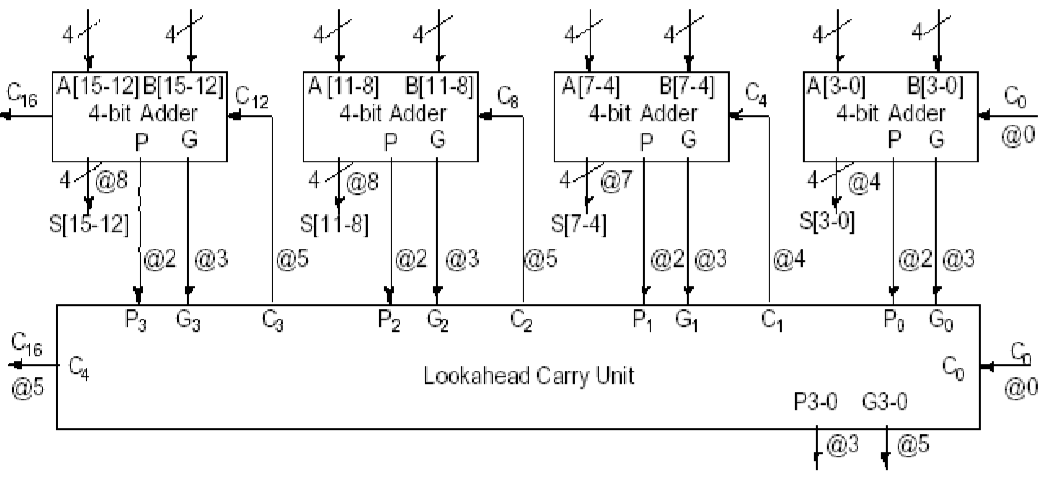
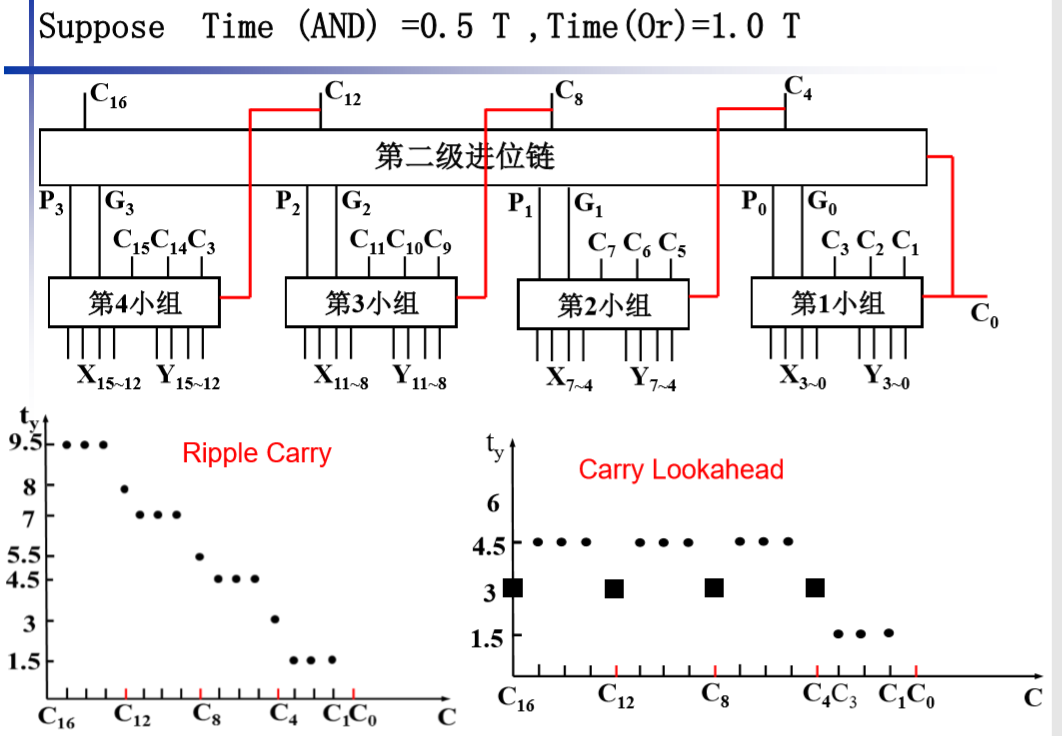
我们对比两种方式:
一、组内使用超前进位,组间串行:如上方左图所示。
二、组内使用超前进位,组间超前进位:如上方右图所示。
多媒体中的饱和操作
当正向溢出时,值保留在最大可表示值。
当反向溢出时,值保留在最小可表示值。
二进制乘法
整数
二进制乘法和十进制乘法的运算是一样的,我们可以看一个例子:

我们可以将这个过程用一个流程图来表示:
graph TD
A(开始计算) --> B{乘数最低位=?}
B --> |最低位=1|C[结果+=被乘数]
B --> |最低为=0|D[被乘数左移一位]
C --> D
D --> E[乘数右移一位]
E --> F{是否进行了32次?}
F --> |否|B
F --> |是|G(结束)
其中,被乘数左移一位,就相当于我们在使用竖式计算十进制乘法时,每过一位都要将新的得数向左移一位一样。而乘数向右移一位实际上就是更换将要检测的位数,这样就可以保证每次都检查最低位就可以了。
定点小数的乘法
方法
假设有两个定点小数:
$$
x = 0.x_1x_2x_3...x_n \
y = 0.y_1y_2y_3...y_n
$$
我们可以将\(x·y\)表示成下面的式子:
$$ \[\begin{align} \begin{array} xx*y &= x(2^{-1}y_1+2^{-2}y_2+...+2^{-n}y_n)\\ & = 2^{-1}(y_1x+2^{-1}(y_2x+2^{-1}(…+2^{-1}(y_{n-1}x+2^{-1}(y_nx+0))…))) \end{array} \end{align}\] $$
据此我们可以得到一个通项公式:
$$
\[\begin{align} \begin{array} . z_0 &=0\\ z_1 &= 2^{-1}(y_nx+z_{0})\\ z_2 &= 2^{-1}(y_{n-1}x+z_{1})\\ ...\\ z_i &= 2^{-1}(y_{n-i+1}x+z_{i-1})\\ ...\\ z_n &= x*y = 2^{-1}(y_1x+z_{n-1}) \end{array} \end{align}\]
$$
所以每次只需要相加两个数,然后向后移一位,且相加的数只有n位,因此不需要2n位的加法器。
示例
计算:\(x = 0.1101,y= 0.1011,x*y = ?\)

流程图
为了方便理解,我做了一个流程图
假设有问题n位定点小数乘法:
graph TD
A(开始) --> B{y最低位是什么}
B --> |y最低一位是1|C[result += x]
C --> D[result右移一位]
B --> |y最低一位是0|D
D --> E[y右移一位]
E --> F{是否进行n次}
F --> |已经进行n次|G(结束)
F --> |没有进行n次|B
乘法优化
我们看到刚才的计算过程,y有多少位就需要做多少个轮次的加法,这样的效率是非常之低的。这里优化的主要思想是:并行。
第一种:阵列乘法
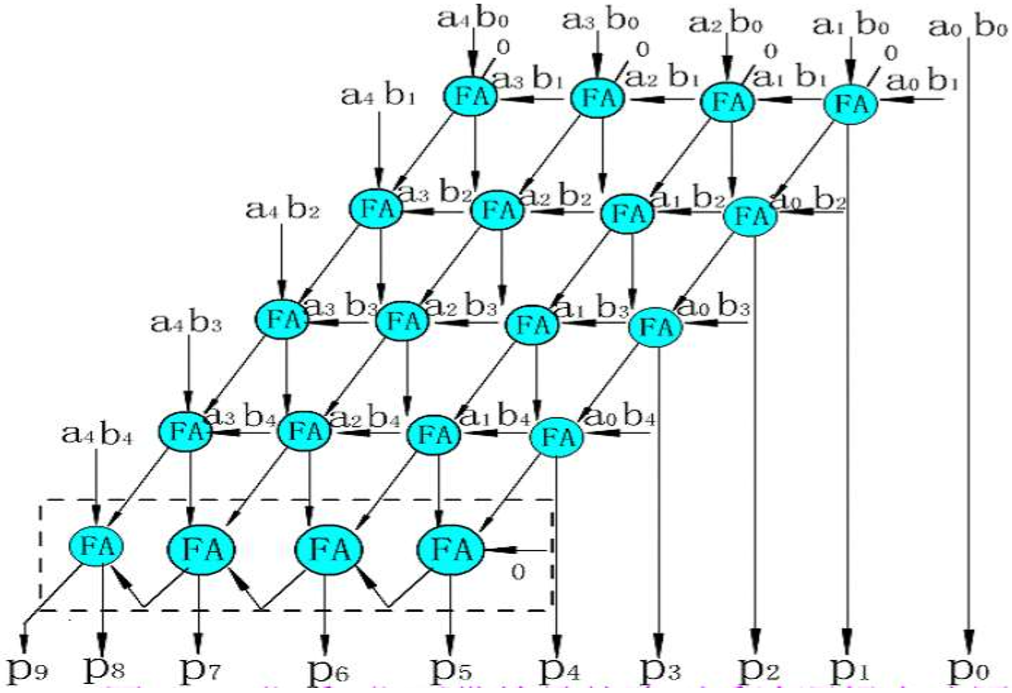
我个人认为,这种乘法器的思想和超前进位的思想有一点相似,它将我们竖式中需要计算的都先计算出来,然后再对他们进行加法即可。
第二种:树型乘法器
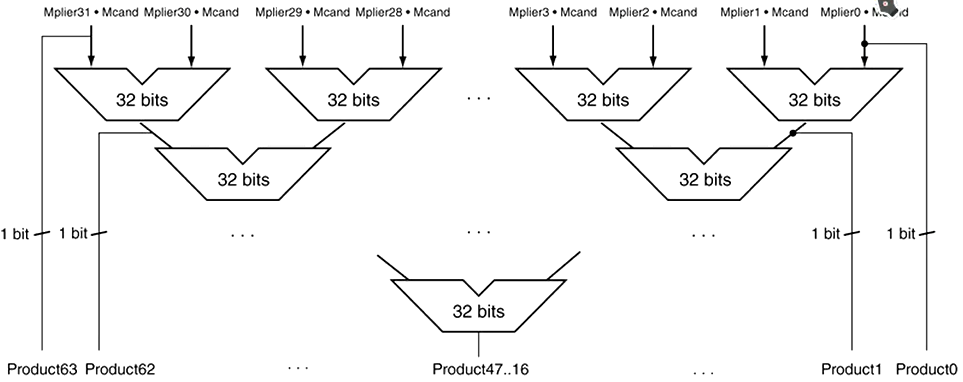
树形乘法器,就是将32位的结果分别算出来,然后再用树形结构进行归并相加,这样就只用\(logn\)级的轮次就可以算出结果。
乘法在MIPS中
在MIPS中,我们将乘法的结果放到了两个专有的寄存器中:
HI:存储高32位
LO:存储低32位
1 |
|
除法
除法及其硬件结构
第一种方法:恢复余数法
算法流程
graph TD
A(开始) --> B[从余数寄存器中减去除数寄存器的内容,将结果放在余数寄存器中]
B --> C{测试余数}
C --> |余数大于等于0| D[商寄存器左移,最低位设为1]
C --> |余数小于0| E[通过给余数寄存器加上除数寄存器内容来恢复原值,结果放在余数寄存器.商同样左移,最低位设为0]
D --> F[除数寄存器右移一位]
E --> F[除数寄存器右移一位]
F --> G{第33次重复?}
G --> |是第33次|H(结束)
G --> |否,小于33次|B
硬件结构
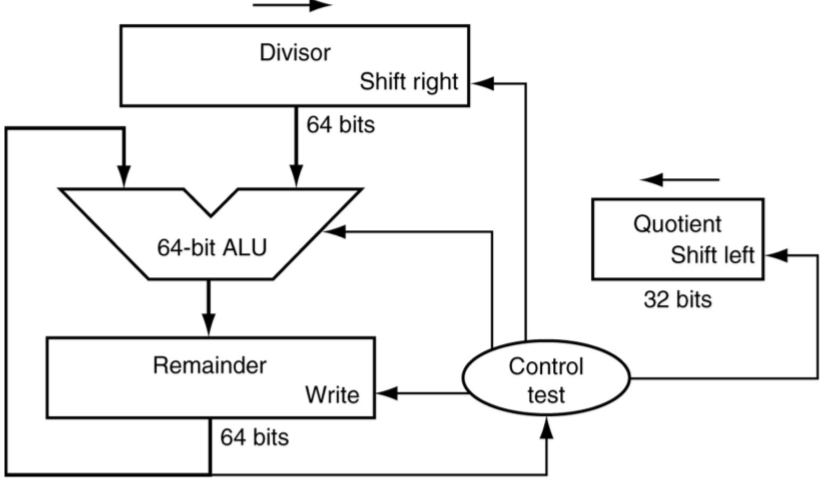
讲解
回复余数法是一种非常暴力的方法,为什么暴力呢,听我慢慢道来:
上面框图一大堆,看起来很麻烦的样子。单核心的操作非常简单,那就是:从高位的解开始尝试,先把余数给减了,如果不行的话,再恢复回来,如果行的话,那就保留。
优化
与优化乘法的方式相似,只用左移余数的方法就可以完成操作,方法如下:
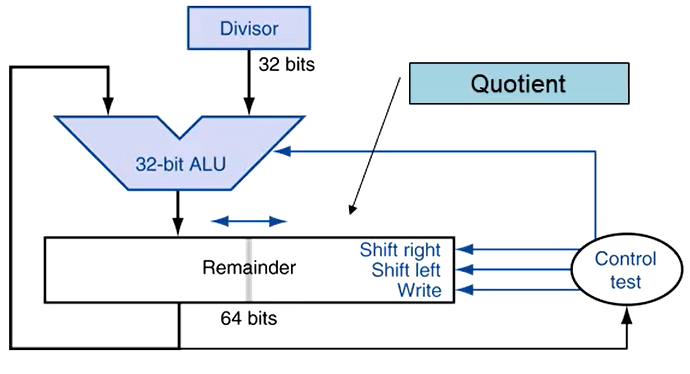
更快速的除法
因为除法中存在减法操作,所以不能像之前的乘法一样优化,但是我们可以通过同时生成多位商的方法进行操作,或是查表法、不执行除法等方法进行优化。
MIPS在除法中
和乘法一样,除法也用到了HI和LO两个寄存器,他们分别用于储存余数、除数。
1 |
|
今天就讲到这里,明天再继续吧。