图形学笔记(三)—— Harris角点检测器
前言
从现在开始学习的是书中的第二章:局部图像描述子。这里主要是寻找图像间的对应点和对应区域。
Harris角点检测器
参考资料
- Jan Erik Solem. Python计算机视觉编程 (图灵程序设计丛书) (p. 33). 人民邮电出版社. Kindle 版本.
- 人工智能:harris角点检测_bilibili
- harris corner detection(角点检测)_bilibili
- 【机器学习】【线性代数 for PCA】矩阵与对角阵相似、 一般矩阵的相似对角化、实对称矩阵的相似对角化_csdn
- 线代022|矩阵的相似对角化 看过有收获,真心分享给大家_bilibili
什么是角点?
说白了就是物体边缘的拐点
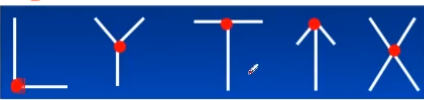
上面图像中的红点处就是角点,有了角点之后,就可以干很多的事情了。
Harris检测角点的核心思路
Harris的核心思路是滑动窗口检测,这里我们将图像中的点分三类进行讨论:
一、平坦点:在图像的某个像素点周围是平坦的,如图所示:
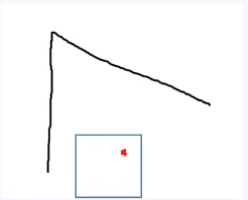
平坦点的周围的像素值没有太大的变化。
二、边缘点:像素点位于一条边上

边缘点的周围的像素向某个方向变化较为剧烈。
三、角点:像素点位于一个角上
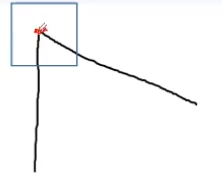
角点的周围各个方向上像素的变化都比较剧烈。
Moravec
知道了这三类情况后,我们来看公式: \[ E(u,v) = \Sigma_{x,y}w(x,y) [I(x+u,y+v) - I(x,y)]^2 \] 其中,\(E(u,v)\)表示竖直和水平方向的偏移,\(w(x,y)\)表示窗口的中心,\(I(x+u,y+v)\)表示中心增加偏移后的灰度值,\(I(x,y)\)表示中心的灰度值。
这个公式就代表着某个点附近的变化的剧烈程度,\(w(x,y)\)是一个滤波(常用高斯)。那么结合上面的理论,这个点的\(E(u,v)\)越大,那么它就越有可能是个角点。但是值得注意的是,这种方法没有旋转不变性。
Harris
泰勒展开
Moravec的缺点是,他只考虑了四种方向,所以他没有旋转不变性。而Harris将方向进行了细化。于是Harris使用全微分的方法将方向进行了细化,具体来说,是用了泰勒展开。
先复习一下什么是泰勒展开: \[ f(x+u,y+v) \approx f(x,y) +uf_x(x,y)+vf_y(x,y) \] 上面的式子是二变量函数的一阶展开,细心如你能发现上面的式子里表示中心增加偏移后的灰度值的式子可以使用泰勒展开!经过一番计算之后可以得到这样一个式子。
计算过程也是非常简单的:
\[ \begin{align*} E(u,v) &= \Sigma_{x,y}w(x,y) [I(x+u,y+v) - I(x,y)]^2 \\ &=w(x,y)\Sigma_{x,y}[I(x,y)+uI_x(x,y)+vI_y(x,y) - I(x,y)]^2 \\ &=w(x,y)\Sigma_{x,y}[uI_x(x,y)+vI_y(x,y)]^2 \\ &=w(x,y)\Sigma_{x,y}[u^2I_x(x,y)^2+v^2I_y(x,y)^2+2uvI_x(x,y)I_y(x,y)] \\ \end{align*} \]
将最终的结果简写一下,就可以得到:
\[ E(u,v) = \Sigma_{x,y}w(x,y) (u^2I_x^2+v^2I_y^2+2uvI_xI_y) \]
矩阵表示
这里\(I_x,I_y\)代表图像在水平、垂直方向上的梯度,我们将这个式子用矩阵来表示(从现在开始就是书上写的了): \[ E(u,v) = [u,v] \left( \Sigma w(x,y) \left[ \begin{matrix} I_x^2&I_xI_y\\ I_xI_y&I_y^2 \end{matrix} \right] \right) \left[ \begin{matrix} u\\ v \end{matrix} \right] \]
最后再来个特殊表示:
\[ E(u,v) = \left[ \begin{matrix} u & v \end{matrix} \right] M_I \left[ \begin{matrix} u\\ v \end{matrix} \right] \]
那么问题来了,我们做了这么多东西,不就是用泰勒展开了一下Moravec的式子,然后用矩阵表示了一下么?我们到底是怎么消除其旋转不变性的呢?
下面来到了这个算法的关键步骤:
相似对角化
我们看到上面的式子\(E(u,v) =\left[\begin{matrix} u & v \end{matrix}\right]M_I\left[\begin{matrix} u \\ v \end{matrix}\right]\)我们使用矩阵相似对角化就可以得到下面的式子: $$
E(u,v) = PP^{-1}
$$
什么是相似对角化?
那么在此之前,我们来复习一下到底什么是矩阵相似对角化呢?(我也忘了)
定义一:设A、B都是n阶矩阵,若存在可逆矩阵\(P\),使得: \[ \begin{align*} P^{-1} AP = B \end{align*} \] 则称为矩阵A和矩阵B相似
定义二:如果方阵A与对角阵相似,则一定存在一个可逆矩阵P,按照下面公式求出方阵A的相似对角矩阵: \[ \begin{align*} \Lambda = PAP^{-1} \end{align*} \]
相似对角化就是求出来这个对角矩阵\(\Lambda\)(好久没碰线性代数了,如果理解有误欢迎指出)
那么怎么算这个\(\Lambda\)呢?在此之前我们需要知道什么样的矩阵能够被相似对角化。 \[ \begin{align*} 一个矩阵可以被特征化 \Leftrightarrow 该矩阵有n个线性无关的特征向量 \end{align*} \] 又有一条件:属于不同特征值的特征向量一定线性无关(这里不能再深挖了,在深挖没完了,有兴趣的自己深挖)
那么根据上面的两个条件,我们可以知道:如果n阶方阵A有n个不相等的特征值,那么说明A可以被相似对角化。而如果A有重特征值,那么检查重特征值对应的线性无关的特征向量的个数若等于特征值的重数,那么就代表A可对角化。另外还有特殊情况:
- 若A为n阶对称阵,那么A可对角化
进行相似对角化
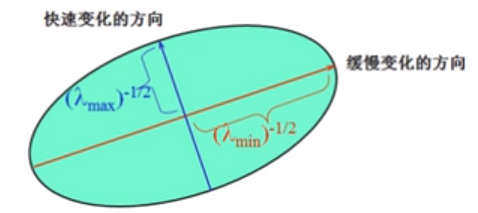
那么根据上面的理论,我们的这个: \[ M_I = \left[ \begin{matrix} I_x^2&I_xI_y\\ I_xI_y&I_y^2 \end{matrix} \right] \] 他显然是一个对称矩阵,所以根据上面的定理他是可以相似对角化的,我们对它使用相似对角化就可以得到上面的式子中的一部分: \[ M_I =P\left[ \begin{matrix} \lambda_1 & 0\\ 0 & \lambda_2\\ \end{matrix}\right]P^{-1} \] 将这部分带入即可得到我们的式子: \[ E(u,v) = \left[ \begin{matrix} u & v \end{matrix}\right]P\left[ \begin{matrix} \lambda_1 & 0\\ 0 & \lambda_2\\ \end{matrix}\right]P^{-1}\left[ \begin{matrix} u\\ v \end{matrix}\right] \] 我们可以先计算\([u\ v]P\)以及\(P^{-1}\left[ \begin{matrix} u\\ v \end{matrix}\right]\),假设得到的结果是\([u'\ v']\)以及\([u'\ v']^T\),那么我们上面的式子就可以改写为: $$ \[\begin{align} \begin{array} E E(u,v) &= \left[ \begin{matrix} u' & v' \end{matrix} \right] \left[ \begin{matrix} \lambda_1 & 0\\ 0 & \lambda_2\\ \end{matrix} \right] \left[ \begin{matrix} u'\\ v' \end{matrix} \right] \\ &= \lambda_1(u')^2+\lambda_2(v')^2\\ &= \frac{u'^2}{\frac{1}{\lambda_1}}+\frac{v'^2}{\frac{1}{\lambda_21}} \end{array} \end{align}\] $$ 好的,到了这里大家打眼一看就知道了,这是椭圆公式啊!那么我们对比一下原来椭圆的公式:\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)在这里我们可以写为:\(a^2 = \frac{1}{\lambda_1}\)那么我们就可以知道\(a = \lambda_1^{-\frac{1}{2}}\),同理可得\(b = \lambda_2^{-\frac{1}{2}}\)
回到问题本身
我们看一些图

如果我们取点附近窗口的梯度的话,我们可以看到:
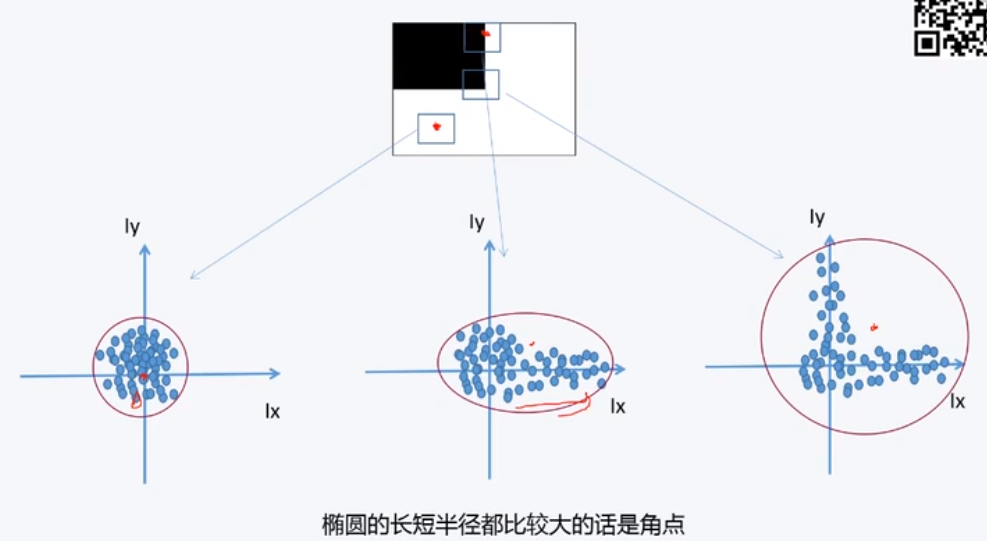
上面的三个图像分别代表:
- 左-平坦点附近窗口内的梯度:离原点普遍较近
- 中-边缘点附近的窗口的梯度:分布在某个坐标轴周围
- 右-角点附近的窗口的梯度:分布在两个坐标轴周围
我们的目标是:让这个椭圆的两个半轴尽量的长,用数学语言来表示就是:让\(\lambda_1,\lambda_2\)尽量的大,有一张图非常的形象:
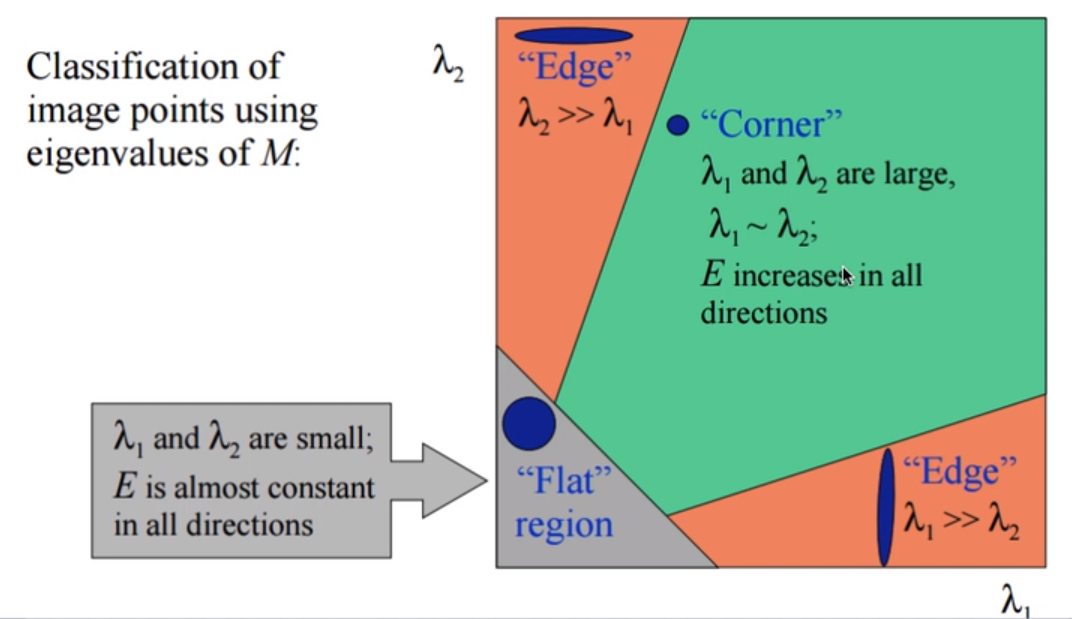
再把我们的目标明确一下:我们希望\(\lambda_1,\lambda_2\)同时很大但又差不多大于是我们构建出了这样的式子: \[ R = det({M_\lambda}) - k trace({M_\lambda})^2 \] 相信很多同学和我一样,已经忘记了这些符号,或者根本没有学过这些符号,那么我来解释一下:
- \(det:\)矩阵的行列式,如果你不知道什么是行列式,那你只能自己百度了
- \(trace:\)矩阵的迹主对角线上各个元素的总和
反应在这个式子里:
- \(M_\lambda = \left[\begin{matrix}\lambda_1&0\\0&\lambda_2\end{matrix}\right]\)
- \(det({M_\lambda}) = \lambda_1\lambda_2\)
- \(trace({M_\lambda})=\lambda_1+\lambda_2\)
所以我们的式子也可以写成: \[ R = \lambda_1\lambda_2 + t(\lambda_1+\lambda_2)^2 \] 如果这个R很大的话,就说明这里是角点,如果这个R很小的话,那么就不是。值得注意的是,这个R评分并不是一个准确的描述问题的机制,拓展一下,这类问题属于病态的问题,也就是说我们无法找到一种准确的方式来描述这个问题,只能通过近似的方式来描述它。放到这个例子里就是我们人眼很容易观测出一个点是不是角点,也可以说出来很多抽象的方法来判断它是否是角点。但之所以我们能够这么轻易的去判断,是因为我们有足够的抽象能力,什么是角点?角点是在角上的点。我们之所以能够如此轻易的判断,是因为我们将角这个概念进行了抽象和封装,而计算机不会。所以我们只能使用像是上面R这种方法来近似地描述问题。(不废话了,继续讲)
实际计算
但是上面说的东西怎么量化的来算呢?我们先计算每个像素点的M矩阵 \[ M = \Sigma w(x,y) \left[ \begin{matrix} I_x^2&I_xI_y\\ I_xI_y&I_y^2 \end{matrix} \right] \] 这里的\(I_x,I_y\)也就是图像在水平、垂直方向的导数,可以用可以用Sobel核去做一个卷积就可以得到。然后这个window函数可以使用高斯核等。该卷积的目的是得到\(M_I\)在周围像素上的局部平均。
可以看到计算的方法很简单,也没啥好讲的,理论懂了就万事大吉了,最终我们使用这两项的比值来衡量这个问题: \[ finalScore = \frac{det({M})}{trace({M})^2} \]
代码
1 | from PIL import Image |
我们使用第一讲里面用到的埃菲尔铁塔试试,原图如下:

使用上述代码提取角点:

可以看到,效果是可以的,但是艾菲尔铁塔的角点太多了,有点难看出来,所以我们换张图来看看。
这是一个象棋棋盘:
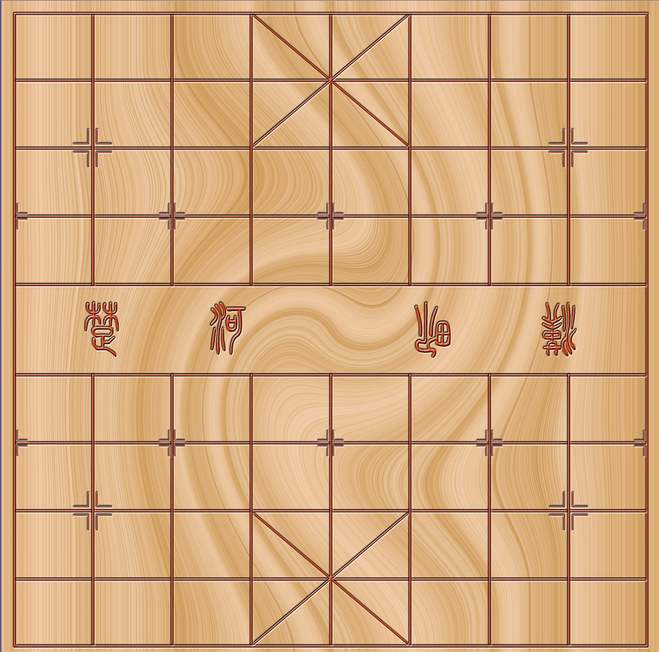
提取效果如下

可以看出提取效果还是非常好的,虽然提取的有点多。其中有的地方提取效果不佳,这有可能是由于后面的纹理导致的。同时我们可以调整阈值进行查看。将阈值调整到0.3,得到的结果如下:
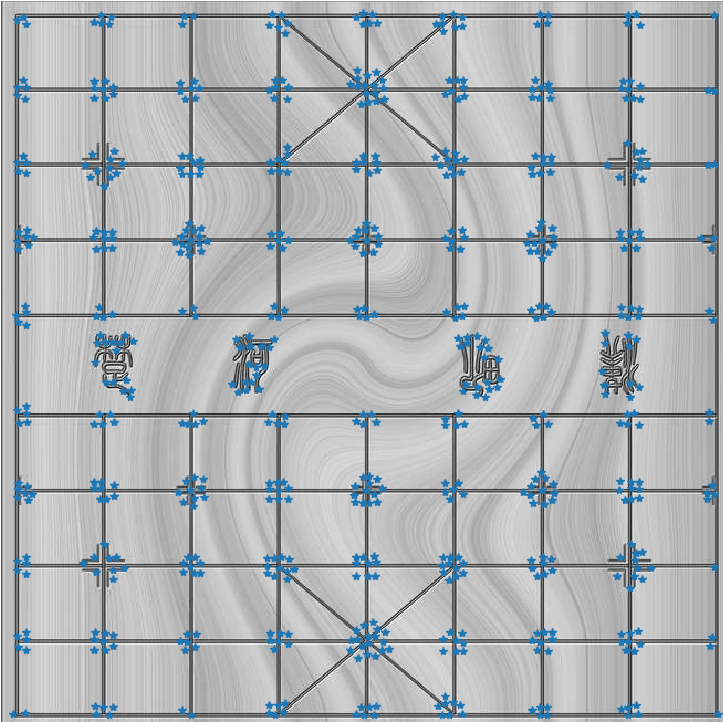
好了,今天就到这里了,这是第二章的第一小节的前半部分,如果只想囫囵吞枣的话,很快就可以水完,但是如果想要抓住事情的来龙去脉,把事情耨清楚,就需要一定的努力了,之前的博客半章4000字就能搞定了,现在一个问题就需要4000字了。
学这个问题也让我理解到,好的参考读物有多么的重要,读那些垃圾博客再多也不如多读一些经典的东西。