python图像处理笔记(二)

图像处理笔记（二）

放在最开始的话

参考的资料

参考的资料是《python图像处理》，所以说学习的顺序和书中的编排也是基本相同的。书中对原理的解析非常少（几乎没有），所以我决定随着看到书中的现象，随着把原理搞清楚，顺便做成文档发到网上，也希望大家能够通过阅读我的文档有所收获。

感谢

今天下午忙完其他的事之后，忽然发现上一篇博客的浏览量有20！写了这么久博客，还从来没这么多人看。昨天讲的SVD有点粗糙，原因是我个人也一知半解，等我的西瓜书到了之后我在再仔细研究一下，再发一篇专门用来讲他们。感谢大家的支持，我会继续写的。

形态学：对象计数

前一阵子看到女朋友再用ImageJ处理叶片数据，结果今天就学到了。

对象计数的过程大体可以分为：

• 将图像转换成灰度图

• 对灰度图进行二值化

• 统计图中值为1的连通块的个数

下面我们对一张图片进行计数，用的图片并非是网络上的开放图片，如果大家想要练习的话，可以从网上下一些相似的图像自己玩一玩，我用到的图象是这个:

大家看到的样子，是他已经缩放到了9%的样子，所以我们知道这张图片的尺寸很大。首先我们将图片以灰度图方式读入，并且进行二值化处理，进行观察。

from PIL import Image

from numpy import *

import matplotlib.pyplot as plt

from scipy.ndimage import measurements, morphology

import modules

def compare(im1, im2, module = 'gray'):

    """

    在一张图里面显示两个图片

    """

    fig, ax = plt.subplots(figsize=(12,8),ncols=2,nrows=1)

    ax[0].imshow(im1, module)

    ax[1].imshow(im2, module)

    plt.show()

im = array(Image.open("C:\\Users\\wangsy\\Desktop\\learning\\cl2\\leafs.jpg").convert("L"))

temp = 1*(im>140)

compare(im, temp)

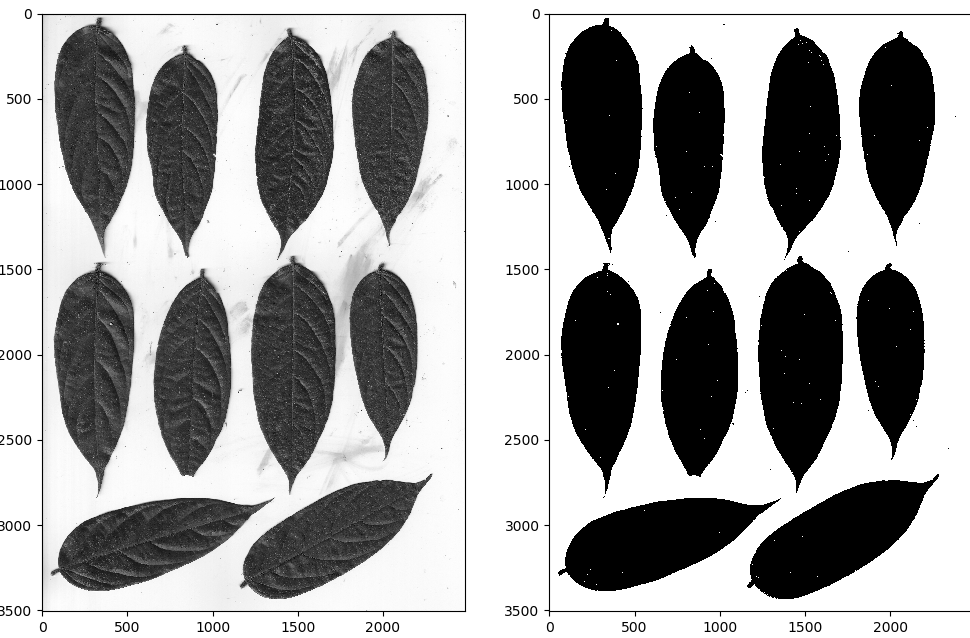
我们可以发现，叶片的形状已经基本呈现出来了，但是比较恼火的是途中的白色处还有零星的噪点（说白了就是本来应该白的地方是黑的），这显然不是我们想要的。这时，我们有几条路去解决这个问题：

• 一、调整二值化阈值：

  二值化是需要一个阈值的，我们这张图是以140为阈值去做的，我们可以尝试调整一下这个阈值，看看能不能达到降噪的目的

  from PIL import Image
  
  from numpy import *
  
  import matplotlib.pyplot as plt
  
  from scipy.ndimage import measurements, morphology
  
  import modules
  
  def compare(im1, im2, module = 'gray'):
  
      """
  
      在一张图里面显示两个图片
  
      """
  
      fig, ax = plt.subplots(figsize=(12,8),ncols=2,nrows=1)
  
      ax[0].imshow(im1, module)
  
      ax[1].imshow(im2, module)
  
      plt.show()
  
  im = array(Image.open("C:\\Users\\wangsy\\Desktop\\learning\\cl2\\leafs.jpg").convert("L"))
  
  temp1 = 1*(im>160)
  
  temp2 =  1*(im>180)
  
  compare(temp1, temp2)

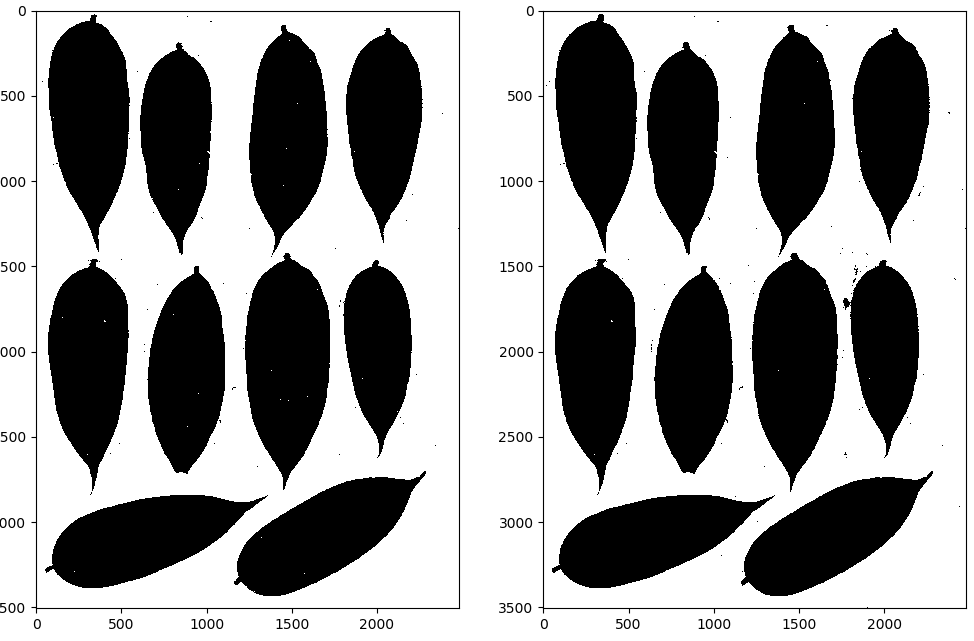
上面的图像分别是以160、180为阈值进行二值化的图像，可以看出来，阈值高了也未必是一件好事，同时二值化的图像无论如何调整阈值都是会存在一定的噪点的。

• 膨胀与腐蚀

  图像的膨胀（Dilation）和腐蚀（Erosion）是两种基本的形态学运算，主要用来寻找图像中的极大区域和极小区域。其中膨胀类似于“领域扩张”，将图像中的高亮区域或白色部分进行扩张，其运行结果图比原图的高亮区域更大；腐蚀类似于“领域被蚕食”，将图像中的高亮区域或白色部分进行缩减细化，其运行结果图比原图的高亮区域更小。——这段话来源于这篇博客

  我们这里主要用腐蚀，腐蚀的主要作用就是：

  • 图像边界收缩

  • 去噪声

  • 元素分割

  他的原理是使用一个结构元扫描这张图片中的每一个元素，如果以当前元素为中心放置结构元的区域中全是1，那么这里就取1，如果不是的话，就取0。结构元是什么呢？实际上和滤波器差不多。说白了就是，有一张图像A，还有一个用于筛选的结构元B。我们以每个A的元素为中心，检查其周围和B一样的区域，如果里面有一个不是1的话，那么这个元素所在位置就是0，反之则为1。

  一般使用opencv完成这个操作，但是为了和教材贴合，我们还是用scipy.ndimage来实现这个操作吧。

  from PIL import Image
  
  from numpy import *
  
  import matplotlib.pyplot as plt
  
  from scipy.ndimage import measurements, morphology, binary_erosion
  
  import modules
  
  def compare(im1, im2, module = 'gray'):
  
      """
  
      在一张图里面显示两个图片
  
      """
  
      fig, ax = plt.subplots(figsize=(12,8),ncols=2,nrows=1)
  
      ax[0].imshow(im1, module)
  
      ax[1].imshow(im2, module)
  
      plt.show()
  
  im = array(Image.open("C:\\Users\\wangsy\\Desktop\\learning\\cl2\\leafs.jpg").convert("L"))
  
  
  
  im = 1*(im<150)
  
  im = modules.imresize(im, (im.shape[1]//6,im.shape[0]//6))
  
  labels, nbr_objects = measurements.label(im)
  
  
  
  im_open = binary_erosion(im, iterations =6)
  
  compare(im, im_open)
  
  labels_open, nbr_objects_open = measurements.label(im_open)
  
  
  
  print(nbr_objects, nbr_objects_open)

  我们使用腐蚀功能对图片进行腐蚀，使用measurements.label对腐蚀后的图片做了统计，下面是两种结果的对比:

  

仔细观察你会发现，腐蚀过的叶片更加瘦小，里面的黑洞洞也更大了，并且旁边的噪点变少了，我们使用统计功能发现：

未腐蚀统计的连通块数目：22

腐蚀过的区域连通块数目：10

可以看出，腐蚀过的区域的连通块数目更加符合我们的预期。当然，在上面的代码中，为了增加程序运行的效率，我使用了之前章节中我们写过的imresize函数对原本很大的图片进行了缩放，图片被缩放了六倍。

当然了，这一部分的问题解决的并不完美，但是由于能力有限，暂时无法全部解决，我会在以后再回来填坑的。

一些有用的Scipy模块

读写.mat文件

你可以使用Scipy来对.mat文件进行读取和存储，操作如下：

读取

data = scipy.io.loadmat('test.mat')

打开的data对象包含一个字典，字典的键表示原来的.mat文件中的变量名，当然你也可以反过来将你创建好的字典进行保存。

保存

data = {}

data['x'] = x

scipy.io.savemat('test.mat',data)

以图像的形式保存数组

因为我们需要对图像进行操作，并且需要使用数组对象来做运算，所以可以直接保存为图像文件。imsave()函数可以从scipy.misc模块载入。要将数组im保存到文件中，可以使用下面的命令：

from scipy.misc import imsave

imsave('test.jpg',im)

这里面也包含了著名的Lena测试图像：

lena = scipy.misc.lena()

woc，这是啥，我快点打开看看。

AttributeError: module 'scipy.misc' has no attribute 'lena'

百度之，发现是这张图：

其实这张图的完整版有点让人大跌眼镜，好奇的可以点这个链接看一下，还是比较惊艳的哈。这背后还有一段八卦，好奇的可以看这里

高级示例：图像去噪

告诉你个好消息，第一章快学完了。

原理

这里使用的是ROF去噪模型。据说他的数学基础和处理技巧都非常高深，所以书里就没讲。但是好在，书中还是有对ROF模型的简述:

一副灰度图像\(I\)的全变差定义为梯度范数之和。在连续表示的情况下，全变差表示为:

$$

J(I) = |I|dx

$$

在离散表示的情况下，全变差表示为：

$$

J(I) = _x |I|

$$

这里的\(I\)就是这张图片，相当于是一个多元函数的自变量。其中上面的式子是在所有图像坐标 \(X = [x,y]\)上取和。在ROF模型中，目标函数为寻找降噪后的图像U，使下式最小：

$$

_{U}||I-U||^2+2J(U)

$$

图形学在研究的问题都是病态的问题，用人话来说就是没法准确表示的问题，所以在早年（AI不火的时候）图形学问题大多都是通过最小化能量函数的方法进行求解的，上面的也是一样。我们观察上面的式子可以发现，这个式子表示：通过调整U,来使得后面的式子达到最小化，后面的式子分为两部分：

• \(||I-U||^2\)上过初中的兄弟萌不难把它和距离公式联系在一起，那么这个就表示新的图U与原来的图I之间的距离，这个距离实质上描述了两张图的差异程度

• \(2\lambda J(U)\) 这部分描述的是图像的平滑程度，我们认为平滑的图像噪声会更小，这一项小的时候噪声会更小。

我们通过权衡这两项来均衡图像的失真程度以及修改后图像的平滑程度，试想如果没有了前一项，那么机器直接生成一张空白的图像就可以溜之大吉。反之，如果只有前面一项，机器直接生成一个和原图完全一样的图片也可以蒙混过关。当然，我们也可以通过调节两项之间的权重来调节生成的图片的效果。

代码

from numpy import *

def compare(im1, im2, module = 'gray'):

    import matplotlib.pyplot as plt

    """

    在一张图里面显示两个图片

    """

    fig, ax = plt.subplots(figsize=(12,8),ncols=2,nrows=1)

    ax[0].imshow(im1, module)

    ax[1].imshow(im2, module)

    plt.show()

def denoise(im, U_init, tolerance = 0.1, tau = 0.125, tv_weight = 100):

    """

        ROF降噪模型

        输入：

            im     : 有噪声的图像

            U_int : 降噪后图像的初始值

        输出：

            去噪和去纹理后的图像， 纹理残留

    """

    # 获取图像的大小

    m, n  = im.shape

    

    # 初始化变量

    U  = U_init

    Px = im # 对偶域的x 分量

    Py = im # 对偶域的y 分量

    error = 1

    iter = 0

    while(error > tolerance):

        iter+=1

        if(iter > 10000):

            break

        if(iter %1000 ==0):

            compare(im,U)

        Uold = U

        # 变量U梯度的x分量

        GradUx = roll(U, -1, axis = 1) - U

        # 变量U梯度的y分量

        GradUy = roll(U, -1, axis = 0) - U

        

        # 更新对偶变量

        PxNew = Px + (tau / tv_weight) * GradUx

        PyNew = Py + (tau / tv_weight) * GradUy

        NormNew = maximum(1, sqrt(PxNew**2 + PyNew**2))

        

        # 更新X、Y分量

        Px = PxNew / NormNew

        Py = PyNew / NormNew

        

        # 更新原始变量

        RxPx = roll(Px, 1, axis = 1)

        RyPy = roll(Py, 1, axis = 0)

        

        DivP = (Px - RxPx) + (Py - RyPy) # 对偶域的散度

        U = im + tv_weight * DivP # 更新原始变量

        

        # 更新误差

        error = linalg.norm(U - Uold) / sqrt(n*m)

    return U, im - U



if __name__ == "__main__":

    from numpy import random

    from scipy.ndimage import filters

    print(1)

    # 使用噪声创建合成图像

    im = zeros((500,500))

    print(1)

    im[100:400,100:400] = 128

    print(1)

    im[200:300,200:300] = 255

    print(1)

    im = im + 30*random.standard_normal((500,500))

    G = filters. gaussian_filter(im, 10)

    compare(im,G)

    U, err = denoise(im,im)

    

    compare(U, err)

    compare(U,G)

结果

这是原来的图片：

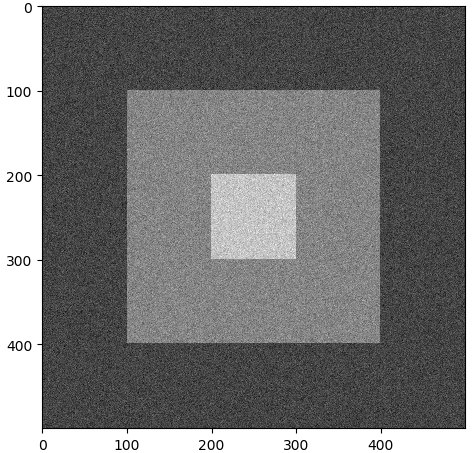
下面的图片中，左边是ROF出来的，右边是高斯出来的：

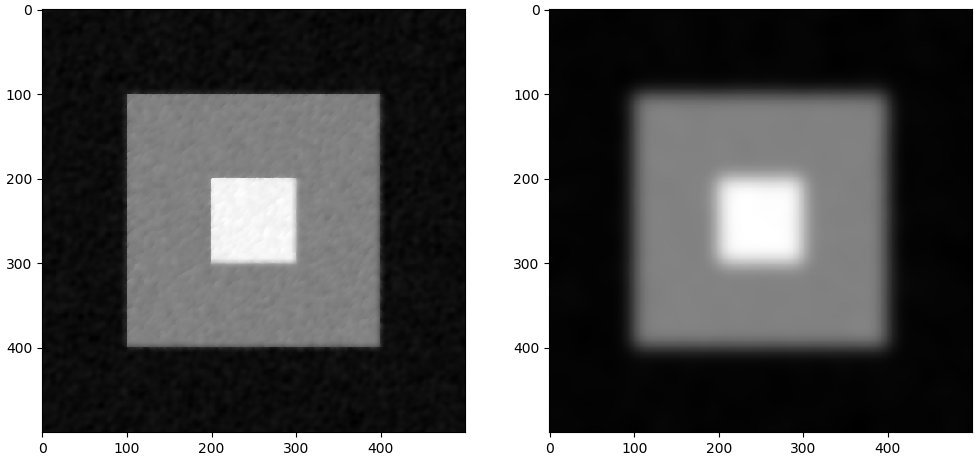
可以看出来，两种方法都是有降噪的作用的，但是两者之间也有所区别：

• 高斯：更像是将图片整体同时都进行了模糊，这样能让图像的平滑都变高，但却无法保留图像的边缘信息。

• ROF：相较于高斯，能够保留图像的边缘信息，但是在某些内部部分它的平滑效果不如高斯好

实际应用

下面我将使用图像平滑技术来P图(这图已经P过了，我再PP看看会咋样)，下面是照片：

可以看到，已经是非常好看的了。

接下来我们先尝试着将它转换成灰度图并且使用ROF进行降噪。

首先先将图片转化成灰度图

接下来，跑我们的ROF降噪模型：

# -*- coding: utf-8 -*-

"""

Created on Wed Apr  8 21:52:32 2020



@author: wangsy

"""





import ROF

from PIL import Image

from numpy import *

import matplotlib.pyplot as plt

from scipy.ndimage import measurements, morphology, binary_erosion

import modules

im = array(Image.open("C:\\Users\\wangsy\\Desktop\\learning\\cl2\\psc.jpg").convert("L"))

print(im.shape)

imNew,_ = ROF.denoise(im,im)



ROF.compare(im, imNew)

发现并没有什么变化。。。为了证明我们这几天的学习是有用的，我决定再给她做一个直方图均衡！

imNew,_ = modules.histeq(imNew)

ROF.compare(im, imNew)

emmmm，不说了，这年头进医院有点危险，我要做好防护了。不行！一定是灰度图的问题，我要这样完成美化任务：

• Step1：使用RGB通道读入图形

• Step2：对每个通道的图形单独进行ROF

• Step3：用生成出来的图片装逼，跳

import ROF

from PIL import Image

from numpy import *

import matplotlib.pyplot as plt

from scipy.ndimage import measurements, morphology, binary_erosion

import modules

im = array(Image.open("C:\\Users\\wangsy\\Desktop\\learning\\cl2\\psc.jpg"))

imNew = zeros((im.shape))

for i in range(3):

    imNew[:,:,i], _ =  ROF.denoise(im[:,:,i],im[:,:,i])

imNew = imNew/255.

ROF.compare(im,imNew)

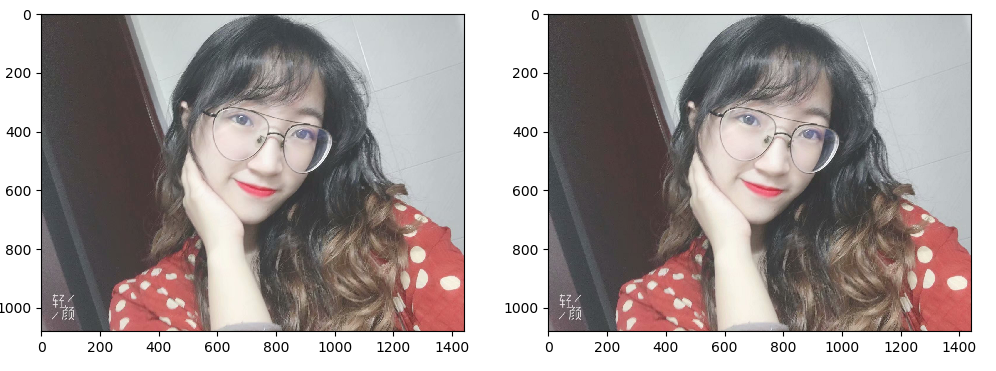
这也没啥差别啊。。啊！你看将图片放大后，右边的也就是P过的图变得更白了呢！（确信）

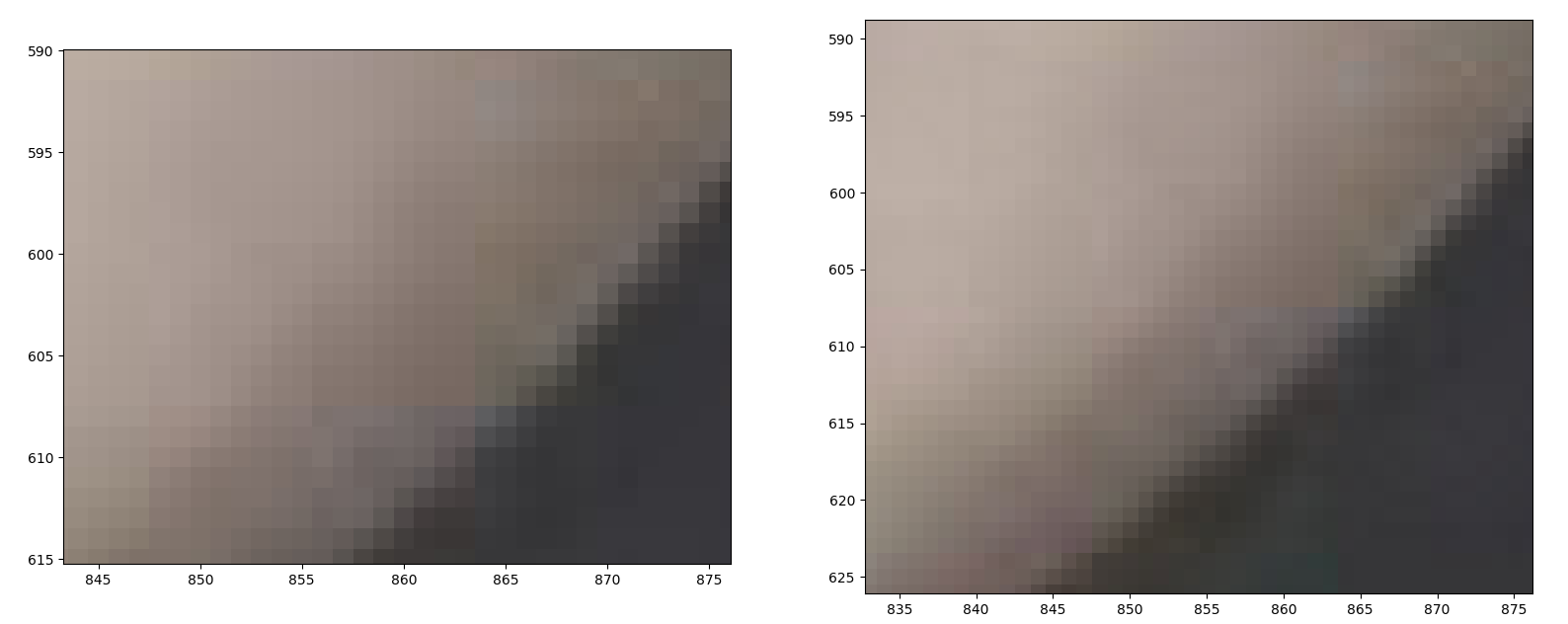
不行，这样的效果不够明显，但是我又不会别的东西，那就在再每一层加个直方图均衡！

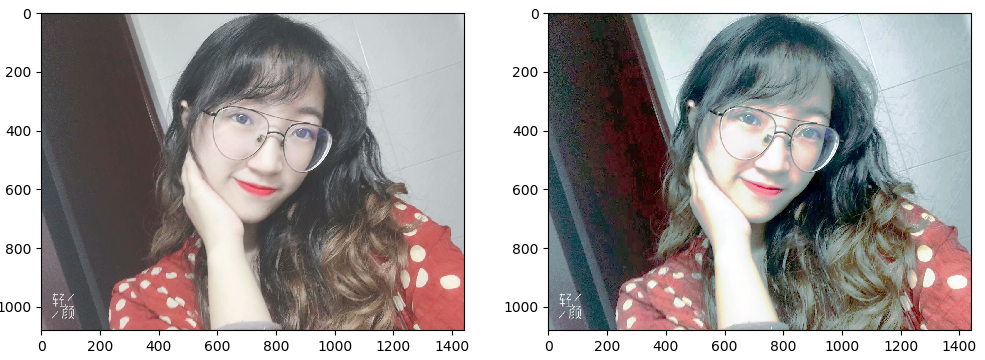
你快看呢！我给你染了个奶奶灰！得了，我没招了GG。

其他真实图片

为什么对于上面的图片，我们的P图ROF没有用了呢？我觉得有以下原因：

• 一、P图软件（轻颜相机）已经对图像进行了降噪，反复降噪效果不大

• 二、由于现代拍摄技术的成熟再加上拍摄场景较为明亮，图片本身噪点就不高

我用我ipad的原相机在漆黑的夜晚拍了一张图片，我们用这张图片再来看一下降噪的效果：

这张照片很大，也很糊，我们需要先把它resize一下，让他小一点，我们好快点处理。

import ROF

from PIL import Image

from numpy import *

import matplotlib.pyplot as plt

from scipy.ndimage import measurements, morphology, binary_erosion

import modules

im = array(Image.open("C:\\Users\\wangsy\\Desktop\\learning\\cl2\\IMG_0551.JPG"))

print(im.shape)

im = modules.imresize(im,(im.shape[0]//3,im.shape[0]//3))

imNew = zeros((im.shape))

for i in range(3):

    imNew[:,:,i], _ =  ROF.denoise(im[:,:,i],im[:,:,i])

    # imNew[:,:,i], _ = modules.histeq(imNew[:,:,i])

imNew = imNew/255.

ROF.compare(im,imNew)

观察上面的图片我们还是看不到太多的区别，但是我们将他们放大：

我们会发现，左边的（原图）噪点明显，而右边的图像则较为平滑。

另外，我想介绍另一个功能，我们对这张图进行直方图均衡化:

import ROF

from PIL import Image

from numpy import *

import matplotlib.pyplot as plt

from scipy.ndimage import measurements, morphology, binary_erosion

import modules

im = array(Image.open("C:\\Users\\wangsy\\Desktop\\learning\\cl2\\IMG_0551.JPG"))

print(im.shape)

im = modules.imresize(im,(im.shape[0]//3,im.shape[0]//3))

imNew = zeros((im.shape))

for i in range(3):

    imNew[:,:,i], _ =  ROF.denoise(im[:,:,i],im[:,:,i])

    imNew[:,:,i], _ = modules.histeq(imNew[:,:,i])

imNew = imNew/255.

ROF.compare(im,imNew)

小区的雨棚、水管、树丛、墙、路都非常清晰的显示出来了！为了再探索一下这个东西，我决定在漆黑的卧室里给我拍个照片，看看用这个做会怎么样！

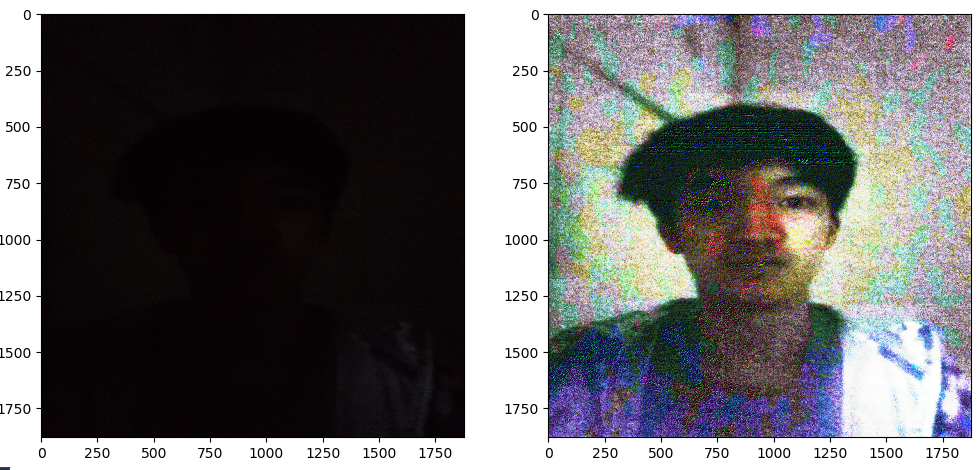
左边是给自己拍的照片，右边是使用直方图均衡化后的照片，属实nb。

• 我装逼：bulabulabula！！！

• 女朋友：哦