最优化技术——线性规划
线性规划基本概念
线性规划问题就是在一组线性约束条件下,求解目标函数最优解的问题
标准形式
线性规划问题的标准形式:
- 目标函数求最大值
- 所有约束条件均由等式表示
- 每个约束条件右端常数常为非负值
- 所有决策变量为非负值
改造方法
所有的情况与改造方法
目标函数求最小值则应该改为求最大值:
方法——添加负号:
\[ min F = \Sigma c_jx_j \rightarrow maxF = -\Sigma c_jx_j\]
约束条件中,某些常数项bi为负数
方法——在约束条件两边乘以负号
\[\Sigma a_{i,j}x_j>-3 \rightarrow -\Sigma a_{i,j}x_j<3\]
约束条件不等式符号为<=
方法——在不等式左边加上一个非负变量(松驰变量)
\[\Sigma a_{i,j}x_j \leq b_i \rightarrow \Sigma_{j=1}^m a_{ij}x_j+x_{m+1}=b_i\]
约束条件不等式符号为>=
在不等式左边减去一个非负变量(剩余变量)
\[\Sigma a_{i,j}x_j \geq b_i \rightarrow \Sigma_{j=1}^m a_{ij}x_j-x_{m+1}=b_i\]
约束条件中某变量有如下限制:
一、某变量必须为负数,即:\[x_j \leq0\]:
方法——设置一个新的变量
\[x_j' = -x_j\]
二、某个变量无符号限制:
方法——将该变量拆分成两个正数的差
\[V_k \geq 0, U_k \geq 0,X_k = V_k - U_k\]
例题
一、
\[min F = -3x_1 + 4x_2 -2x_3 + 5x_4\]
\(s.t.\)
\[4x_1 - x_2+2x_3-x_4=-2\]
\[x_1+x_2+2x_3-x_4 \leq14\]
\[-2x_1+3x_2-x_3+2x_4\geq2\]
\[x_1\geq0,x_2\leq0,x_3\geq0\]
将上面的式子化成标准型,首先需要检查上面的式子中有哪些地方不符合我们的要求:
- 目标函数为最小值\[min F = -3x_1 + 4x_2 -2x_3 + 5x_4\]
- 等式约束右边为负数\[4x_1 - x_2+2x_3-x_4=-2\]
- 不等式约束\[x_1+x_2+2x_3-x_4 \leq14\],\[-2x_1+3x_2-x_3+2x_4\geq2\]
- 约束中有小于零的\[x_1\geq0,x_2\leq0,x_3\geq0\]
额,经过整理我们发现。。。都不符合,所以需要一条一条的改:
| 改前 | 改后 |
|---|---|
| \[min F = -3x_1 + 4x_2 -2x_3 + 5x_4\] | \[maxS=-minF = 3x_1-4x_2+2x_3-5x_4\] |
| \[4x_1 - x_2+2x_3-x_4=-2\] | \[-4x_1+x_2-2x_3+x_4 = 2\] |
| \[x_1+x_2+2x_3-x_4 \leq14\] | \[x_1+x_2+2x_3-x_4+x_5 =14\] |
| \[-2x_1+3x_2-x_3+2x_4\geq2\] | \[-2x_1+3x_2-x_3+2x_4 -x_6= 2\] |
| \[x_2\leq0\] | 设\[x_7 \geq 0 , x_7 = - x_2\] |
| \[x_4 \]无约束 | 设\[x_8,x_9\geq0,x_4 = x_8-x_9\] |
整理之后得到:
\[maxS=-minF = 3x_1+4x_7+2x_3-5x_8+5x_9\]
\(s.t.\)
\[-4x_1-x_7-2x_3+x_8-x_9 = 2\]
\[x_1-x_7+2x_3-x_8+x_9+x_5 =14\]
\[-2x_1-3x_7-x_3+2x_8-2x_9 - x_6= 2\]
\[x_i \geq 0,j=1,3,5,6,7,8,9\]
概念之凸集
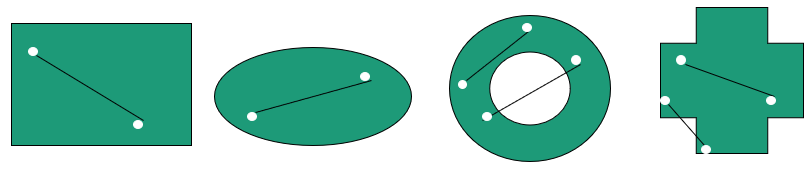
- 凸集:如果集合C中任意两点\[X_1,X_2\],其连线上的所有点也都是集合C中的点,称C为凸集。
- 有限个凸集的交集仍然是凸集
- 顶点:如果凸集C中不存在任何两个不同的点\[X_1,X_2\],使\(X\)成为这两个点连线上的一个点。
 ## 线性规划的一些定义
## 线性规划的一些定义
定义一:凡是满足\[Ax=b\]及\[x\geq0\]的解\[x = (x_1,x_2,..,x_n)^T\]称为线性规划问题的可行解。同时满足\[max Z = cx\]的可行解称为最优解
定义二:设线性规划约束方程组的系数矩阵\(A_{m*n}\)的秩为\(m\),则\(A\)中某\(m\)列组成的任一个\(m\)阶可逆阵\(B\)称为该线性规划问题的一个基矩阵,简称基。若记\(B=(p_1,p_2,…,p_m)\),则称\(p_k(k=1,2,…m)\)为基B中的一个基向量。则A中其余n-m个列向量为非基向量。
感觉这里很象最大线性无关组。
定义3:当\(Ax=b\)式中A确定了一个基B后,与基向量\(p_k\)相对应的决策变量\(x_k\)称为关于基B的一个基变量,而与非基向量所对应的决策变量称为非基变量。
定义4:设\[B=(p_{k_1},p_{k_2},…,p_{k_m})\]是A中的一个基,对应的基变量为\[x_{k_1},x_{k_2},…,x_{k_m}\],我们称非基变量的取值均为零且满足约束条件的一个解x,为关于基B的一个基本解。
解的确定
基本解的确定
B为一个基矩阵,\[X_B\]为对应的基变量, \(N\)为非基矩阵,\(X_N\)为对应的非基变量,那么\[Ax=b\]可以写成: \[ BX_B+NX_N=b \] 由这个式子可以推出: \[ X_B = B^{-1}b-B^{-1}NX_N \] 同时,根据基本解的定义,非基变量的解都是0,所以,最终的解是: \[ \left[ \begin{matrix} X_B\\ X_N \end{matrix} \right] = \left[ \begin{matrix} B^{-1}b\\ 0 \end{matrix} \right] \] 这样的解也被称为关于基B的基本解,同时有定义五:
- 满足非负条件\(x\geq0\)的基本解称为基本可行解
例题
求下列方程组的一个基本解、基本可行解
\[x_1 + 2x_2 \leq 8\]
\[x_2\leq 2\]
解:
首先将他化成标准形式
\[x_1+2x_2 +x_3 = 8\]
\[x_2+x_4 = 2\]
根据上方方程得到系数矩阵:
\[A=\left[\begin{matrix}1 & 3 & 1 & 0\\0 & 1 & 0 & 1 \end{matrix} \right]\]
取前两个列向量作为基向量,后两个就是非基向量
\[B = \left[ \begin{matrix}1 & 2 \\ 0 &1 \end{matrix} \right]\]
令非基变量\[x_3, x_4 = 0\],可以得到基本解
\[(4,2,0,0)^T\]
图解法
假设解以下问题
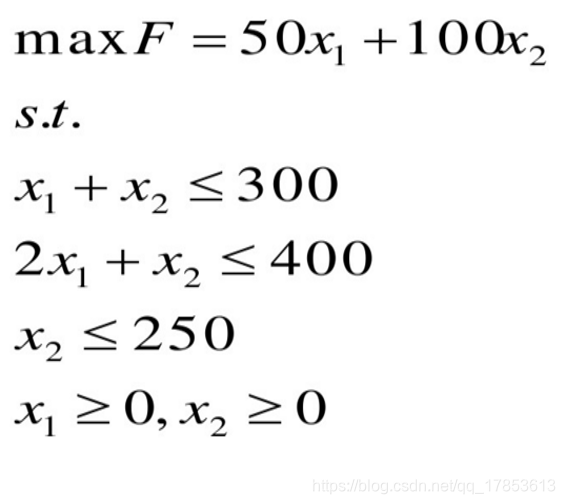
我们可以用图解法的方法解决(初中生就会的那种)
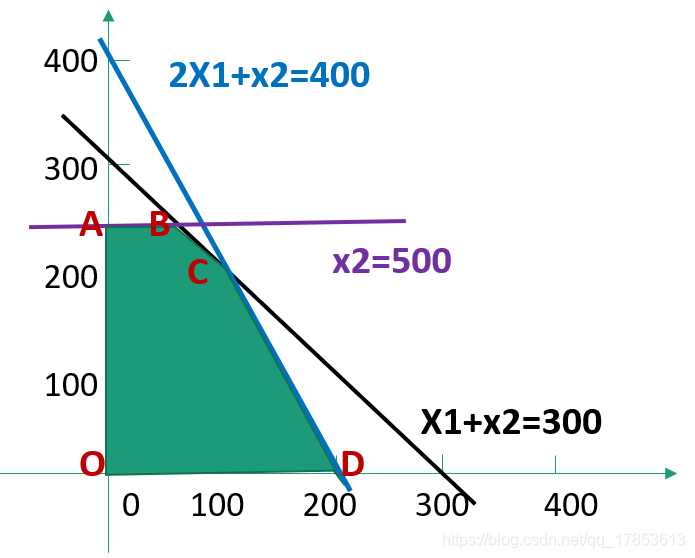
关于图解法的一些定理:
- 定理一:若线性规划问题存在可行解,则该问题的可行域一定是凸集
- 定理二:线性规划问题的基本可行解X对应可行域(凸集)的顶点
- 定理三:若问题存在最优解,一定存在一个基本可行解是最优解
看到定理二忽然恍然大悟,原来我初中铤而走险,每次都只试交点的方法是有科学依据的(逃
定理三也非常有意义,因为它直接给我们提供了一种解决优化问题的方法:找出所有基本可行解然后再一个一个比较,直接得到最大的,但是可惜的是,这样的做法时间复杂度过高,电脑有点遭不住。