组成原理第二章

发表于 | 分类于 |

计算机指令

算术运算指令

1
add a, b, c# a = b + c

设计原则一——对指令进行规整化设置

  • 简化实现
  • 获得更高的性能，更低的成本

代码示例

  • C语言代码
1
f = (g + h) - (i + j)
  • MIPS
1
2
3
add t0, g, h # temp : t0 = g + h
add t1, i, j # temp : t1 = i + j
sub f, t0, t1 #final: f  = t0 - t1

参与算术逻辑运算的变量必须是寄存器变量，对于MIPS(x 32)指令集来说，有32个寄存器，每个寄存器长\[32bit\]，它们：

  • 用于存储最常用到的变量
  • 每个寄存器的编号为0~31
  • 每个寄存器中32位数据称作一个字

约定符号：

  • $t0,$t1,...,$t9 用于表示临时变量
  • $s0,$s1,...,$s 7表示需要保存的变量

设计原则二——更小就会更快

  • 倾向于将算术运算放到寄存器中运行，以加快速度
  • 内存的存储单元通常是百万级的

前面的代码，根据约定符号进行矫正：

1
2
3
add $t0, $s1, $s2
add $t1, $s3, $s4
sub $s0, $t0, $t1

可以看到，在\(MIPS32\)指令集中，只有\(32*32\)个存储空间，这并不足以支持所有运算，所以很多的数据是存储在内存中的，我们将这些被储存在内存中的数据称为_Memory Operands。内存的操作数是用来保存复杂的操作数，这是由寄存器的空间过小导致的。

算数逻辑运算不能直接对内存中的数据进行运算，这就需要我们先从内存中读取(load)数据,然后再进行处理，最终再将操作的结果写入(write)内存。在对内存的操作中，都是通过字节寻址的(每八位分配一个地址)。值得注意的是，每个字节由\(8bit\)组成，而寄存器中每一位长度是\(32bit\)，这就表明，我们在知道首地址的情况下，想要寻找第\(i\)个元素时，需要将偏移量\(*4\)。

MIPS中数据的对齐方式是：大端对齐。什么是大端对齐呢？

  • 存储一个数据，需要四个字节，这也就对应着内存上的四个存储单元。
  • 这四个存储单元有他们相应的标号
  • 高内存地址放整数的低位，低内存地址放整数的高位，这种方式叫正着放，术语叫大端对齐
  • 与大端对齐相反的是小端对齐，说白了就是反着存

Memory Operand 小例子

C code

1
g = h + A[8]

其中，$s1 is g,$s2 is h,$s3 is the base address of A

MIPS code

1
2
lw  $t0, 32($s3) # 读取A[8]，32来源于偏移量*4 = 8*4 = 32
add $s1, $s2, $t0

Memory Operand 小例子2

C code

1
A[12] = h + A[8]

其中，$s2 is h,$s3 is the base address of A

MIPS code

1
2
3
lw  $t0, 32($s3)
add $t0, $s2, $t0
sw  $t0, 48($s3)#写入

可以看出，寄存器和内存的交互主要通过\(lw\) ,\(sw\)两条语句，进行数据的读取、写入，对于编译器而言，选择哪些变量放到寄存器中，哪些放到内存中，是非常关键的问题，同时也是非常困难的问题。

立即数

所谓立即数，即所使用的变量是一个常数，他是包含在指令中的。如:

1
addi $s3, $s3, 4

这就相当于C语言中的

1
s3 += 4;

立即数操作中没有减法，因为减掉一个数就相当于加上这个数的相反数，即：

1
addi $s3, $s3, -4

就可以完成C语言中如下功能

1
s3 -= 4;

支持的数字范围：立即数操作的常亮仅支持有符号的16位整数，即：\(\left[ -32768, 32767\right]\)这个区间。如果需要一个32位整数，那么这个整数就只能被先放到内存中，然后再被寄存器读取。

这里就引出了第三个设计原则：加快高概率事件(Make the Common Case Fast)

  • 小的常数是常用的

  • 使用常用的数，不需要从内存中读取

    数字的类型

  • 无符号整数(unsigned int)

    • 用于表示地址
    • 或是非负数

  • 有符号整数

    • 正负数

  • 浮点数

    • 单精度浮点数(float)
    • 双精度浮点数(double)

有符号数的表示

  • 补码
  • 源码

补码和源码之间有+0和-0的区别。

MIPS中特殊的取值——0

MIPS中0号寄存器永远为0，只能读取，不能写入。我们常用$zero来代表上述的零号计算器，利用这个寄存器，我们可以进行下面的操作：

1
2
add  $t2, $s1, $zero
addi $t2, $zero, 100

事实上，MIPS中是没有初始化的方法的，在上面的代码中，我们用$s1的值初始化了$t2，然后将100赋值给$t2，这种语法的设计减少了很多冗余的语句。

有符号数和无符号数的表示

无符号二进制数计算公式: \[ x = \Sigma \left( x_i 2^i\right) \] 这个老掉牙了，没啥好说的，一个长度为n的无符号二进制数，能表示\(\left[0,2^n-1\right]\)这个区间内的整数。

有符号数的表示：

  • 源码的表示：最高为作为符号位
    • 0代表符号为正
    • 1代表符号为负
  • 源码表示存在的问题：同时存在正0和负0

补码的表示：这一部分我之前看的时候基本上都是硬背的，现在听到这种讲法才恍然大悟（菜是原罪）

假设补码表示的二进制数有n位，标号为\(0 ,n-1\)，那么补码到十进制数的计算公式为： \[ x = -x_{n-1}*2^{n-1} + \Sigma_{i=0}^{n-2} \left(x_{i}*2^{i}\right) \] 它对应的取值范围是:\(\left[ -2^{n-1},+2^{n-1}-1\right]\)

在整数运算中，大多数情况下，使用的是补码的形式。下面有一些特殊的补码数字（帮助理解用的，不用想哪里特殊）:

十进制 二进制
0 0000 0000 ... 0000
-1 1111 1111 ... 1111
最小的数 1000 0000 ... 0000
最大的数 0111 1111 ... 1111

一般情况下，MIPS指令集下的运算都是对有符号数进行运算，除非你显式的告诉计算机要进行无符号数运算，需使用addu操作。

常见操作：

  • 将数字取反：将数字的每一位取反，再对最后一位加1。
    • 优点：可以用已有的加法电路，做简单的拓展即可作为减法电路使用。
  • 符号位扩展：
    • 应用场景：如:使用\(addi\)指令时，得到的是一个16位数字，要将该数字拓展为32位数字，才可以与其他数字进行算术运算。
    • 无符号数的拓展方法：
      • 直接补零
    • 有符号数的拓展方法：
      • 正数：在数字前方补0
      • 负数：在数字前方补1

指令的表示

还记得我们第一章的时候讲过，汇编语言多数时间执行着将高级语言翻译成机器语言(machine code) 工作。下面是一些寄存器名称和用途的的对应表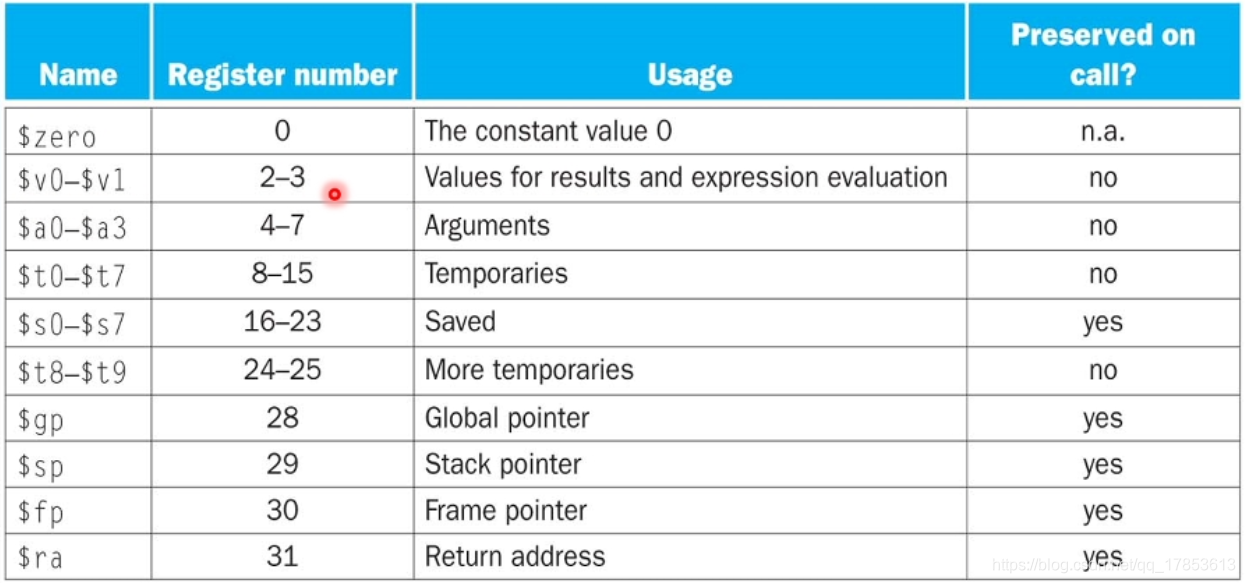： 在这里插入图片描述 其中，1号寄存器被称为$at，它是为汇编程序预留的；26-27号寄存器被称为$k0,$k1，他们是保留给操作系统的。

指令集分为六大类：

  • 算数逻辑运算
  • 内存访问
  • 分支和跳转指令
  • 浮点运算指令 --使用协处理器完成
  • 内存管理指令
  • 特殊指令

0-31号寄存器是我们（程序员）能够访问的到的寄存器，还有我们访问不到的寄存器：

  • PC：用于存放当前程序正在执行的指令
  • HI & LO：在乘除法运算时做临时储存

mips32中指令集架构的格式

在这里插入图片描述 #### R format

主要用途：用于表示算数逻辑运算，分为：

他们分别代表：

  • op：\(operation\ code\)用于表示当前的操作类型
  • rs,rt：表示用于运算的两个源操作数，对应寄存器的编号
  • rd：目标操作数，对应寄存器的编号
  • shamt：针对移位运算，记录移位的次数
  • funct：是opCode的拓展

例子：

1
add $t0, $s1, $s2

对应的指令为：

special $s1 $s2 $t0 0 add
0 17 18 8 0 32
000000 10001 10010 01000 00000 100000

I format

在这里插入图片描述 I-format可以用于之前的\(addi\)操作、\(load/store\)或是条件跳转等指令。 其中

  • rs/rt ：源操作或目标操作寄存器
  • \(constant\ or\ address\)
  • 在进行运算时：补码形式的二进制数
  • 在进行寻址时：表示内存地址

设计规则四——Good design demands good compromises

这种设计方法看似折中、不利于译码，但将长度固定在了３２位，为了统一，增加了一部分译码的复杂性，达到了整体的统一，同时，这种设计方法，降低了后期电路设计的复杂性。

J format

后面再讲

冯诺依曼计算机设计的两个关键特性

１．指令和数据都是二进制串，无法区分

２．程序时能够被改写的

在这里插入图片描述
在这里插入图片描述

存储程序相关的基本概念：

  • 程序可以被保存为二进制文件，这样的特性使得一个程序可以从一个电脑搬到另一个电脑上使用，这一个叫做“二进制的兼容性”（deepin-wine）

  • 为了保证对已经编译好了的软件的继承，指令集架构应当围绕着少数几个大的指令集架构发展。

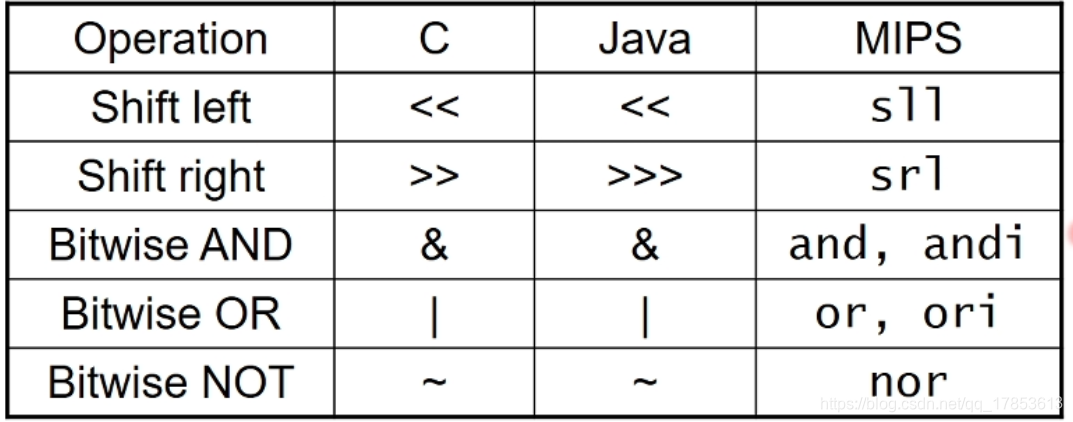
    逻辑运算指令

    一些对应的语言： 在这里插入图片描述

    移位运算(Shift Operations)

special rs rt rd shamt funct
6 bits 5 bits 5 bits 5 bits 5 bits 6 bits

C语言中 

1
2
$s1 = $s2 << 10;
$s1 = $s2 >> 10;
与MIPS中： 
1
2
sll $1,$2,10
srl $1,$2,10
相同 其中： shamt-用于记录移动多少位

  • 逻辑左移运算：

    • 左移，并将空出来的部分用零填充
    • 左移\(i\)位，相当于乘上\(2^i\)

  • 逻辑右移运算：

    • 右移，并将空出来的部分用零填充

    • 右移\(i\)位，相当于除以上\(2^i\)

      与、或运算(And/Or Operations)

      1
      2
      and $t0, $t1, $t2#t0 = t1 and t2
      or    $t0, $t1, $t2#t0 = t1 or     t2

      将$t1 & $t2的值赋给$t0，与运算可以运用在屏蔽寄存器中。

NOR运算

NOR就是not，or，这是一个三目运算符，使用方法如下:

1
nor $t0, $t1, $t2

这个运算表示\(not\ \left( t2\ or\ t1\right)\) MIPS中没有单独的取反操作，如果想要对$t1取反存入到$t0中，方法如下：

1
nor $t0, $t1, $zero

在上述代码中，进行的是\(not\ \left( t1\ or\ zero\right)\)的操作，其中，任何一个数和零进行或运算，还是他本身，再对它本身取反就可以得到\(not\ t1\)的结果。

条件指令（分支与循环）

常见的控制指令：

1
2
3
beq re, rt, L1
bne rs, rt, L1
j          L1

他们对应的C语言语法是:

1
2
3
4
5
6
7
8
9
10
#beq re, rt, L1
if(re == rt){
    goto L1; 
}
#bne rs, rt, L1
if(re != rt){
    goto L1; 
}
#j          L1，无条件跳转
goto L1;

跳转的目标指令，与当前的beq/bne之间，不能超过正负\(2^{15}\)，同时，在写C和C++的时候除特殊情况外应当避免/减少goto语句的使用，因为使用goto语句不当可能会让程序表意不明，更加混乱。

一个小例子（选择结构）

老规矩，先看C/C++

1
2
3
4
5
if(i==j){
    f = g + h;
}else {
    f = g - h;
}

对应的MIPS

1
2
3
4
5
6
          #s3 is i, s4 is j, s0 is f, s1 is g, s2 is h.
          bne $s3, $s4, Else#判断i,j是否相等，若不等就直接跳过下面两行
          add $s0, $s1, $s2#若相等，就继续执行到这一行，完成f=g+h
          j Exit#执行完f = g - h之后跳过下一条语句直接退出
Else: sub $s0, $s1, $s2#执行f = g - h
Exit:

从上面的代码中可以看出，MIPS的标记本身并没有改变代码的执行顺序，仅仅是对某行代码做了标记而已，如果没有\(j,bne,beq\)三条语句的话，就算程序中有标记，MIPS还是会顺序执行的。

第二个例子（循环结构）

Ccode

1
while(save[i] == k) i += 1;

MIPS Code

1
2
3
4
5
6
7
8
 #i is $s3, k is $s5, 地址被保存在$s6中
 Loop: sll $t1, $s3, 2 #偏移量 = i * 4
              add $t1, $t1, $s6# 当前地址= 起始地址 + 偏移量
              lw $t0, 0($t1)#读取数据到t0
              bne $t0, $s5, Exit
              addi $s3, $s3, 1# s3 = s3 + 1
              j  Loop
Exit:

没啥好讲的了，自行体会。

更多条件指令

MIPS Code

1
2
slt rd, rs, rt
slti rt, rs, constant

C Code

1
2
3
4
5
6
7
8
9
10
11
12
#slt rd, rs, rt
if(rs < rt ){
    rd = 1;
}else {
    rd = 0;
}
#slti rt, rs, constant
if(re < constant){
    rd = 1;
}else {
    rd = 0;
}

这个语句可以和beq一起用，来进行在大于、小于等情况下的选择结构。

小练习

1
2
3
4
5
if(i>=j){
    i = i + 1;
}else {
    j = j + 1;
}

将上述代码转化成mips指令集中的code，i,j-->$s1,$s2 我的答案：

1
2
3
4
5
6
           slt    $t0, i, j # if i>=j 0
           beq $t0, $zero, Else #if t0==zero --> i>=j goto Else:j=j+1,else go on
           addi $s1, $s1, 1
           j         Exit
Else: addi $s2, $s2, 1
Exit: ...

有符号和无符号数字的比较

无符号数进行比较： sltu,sltui，其实说白了就是后面加个u就是无符号数操作，再加个i就是常数操作。

函数的调用和函数的返回

基本块，是一个指令序列，在这个序列中是没有分支指令的，也没有其他分支指令的跳转指令。 在这里插入图片描述

函数调用的基本步骤：

  • 将函数相关的参数放入寄存器中(load 指令或者是逻辑运算指令)
  • 将寄存器的控制权交给函数相关的进程。关键
  • 申请，并获得存储空间（堆栈）
  • 执行函数中的指令
  • 将返回的结果放回寄存器中关键
  • 将结果返回到调用的地址中
1
jal ProcedureLabel

将寄存器控制权交给相关的进程： 将ProcedureLabel的下一个地址放到$ra中，然后跳转到目标地址。（这里$ra用于记录返回值返回到哪里）

1
jr $ra

将$ra复制到程序计数器中，这条语句也可以用于其他的跳转用途。

这段他讲的好抽象，我有点没听懂。 下面有一个实例。

Leaf Procedure Example（不调用其它函数的函数）

C Code

1
2
3
4
5
int leaf_example(int g, int h, int i, int j){
    int f;
    f = (g + h) - (i + j);
    return f;
}

我就直接贴最后的代码了：

1
2
3
4
5
6
7
8
9
10
leaf_example：
    addi $sp, $sp, -4#压栈，往下压四个字节
    sw $s0, 0($sp)#将s0放入压好的栈中
    add $t0, $a0, $a1
    add $t1, $a2, $a3
    sub $s0, $t0, $t1
    add $v0, $s0, $zero#将结果放入用于返回的参数$v0中
    lw $s0, 0($sp)#恢复$s0
    addi $sp, $sp, 4#恢复堆栈位置
    jr $ra#返回

说实话，除了jr都看懂了，那个确实没看懂。

None-Leaf Procedures（函数的嵌套调用）

调用者需要将一些信息存储到堆栈中：

  • 被使用的寄存器($s0-$s7)
  • 他的返回地址
  • 在函数、过程中用到的临时变量 在返回之前，将堆栈中数据取出进行恢复。
1
2
3
4
5
6
if fact(int n){
    if(n < 1){
        return 1;
    }
       return n*fact(n-1);
}

对应的mips,参数n放到$a0中，结果放到$v0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
fact:
    addi $sp, $sp, -8
    sw $ra, 4($sp)
    sw $a0, 0($sp)
    slti $t0, $a0, 1#判断是否小于1
    beq $t0, $zero, L1#如果大于等于1，那么跳到后面去
    addi $v0, $zero, 1#如果小于1，那么将1付给v0
    addi $sp, $sp, 8#从栈空间中出栈两个
    jr $ra#返回
L1:
    addi $a0, $a0, -1#减一
    jal fact# 从新跳转到fact部分去执行
    lw $a0, 0($sp)#将堆栈中把两个参数取出
    lw $ra, 4($sp)
    addi $sp, $sp, 8#恢复堆栈
    mul $v0, $a0, $v0#相乘
    jr $ra#返回

栈上的变量

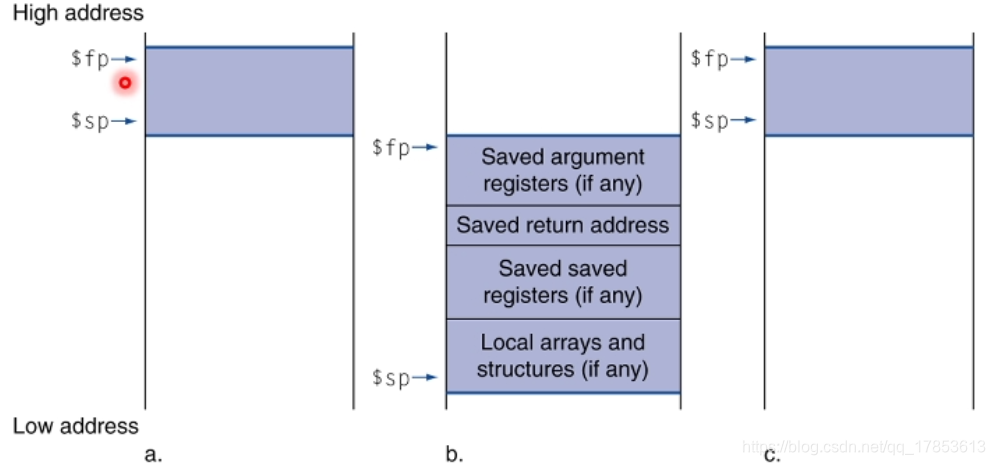在这里插入图片描述 堆栈用于存储临时变量。 图中$sp指向堆栈可用地址，申请栈的时候，向下申请。$fp的存在使得便于恢复栈。

内存中一个程序分为不同的段：

  • 代码段：用于存放指令
  • 静态数据：执行过程中不会变的数据
  • 堆：C语言中new出来的东东，需要手动释放
  • 栈：临时变量

思考：

  • 递归能否转循环
    • 答案是可以的，就直接模拟它的栈